
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 在同一条直线上,连结
在同一条直线上,连结![]() .
.
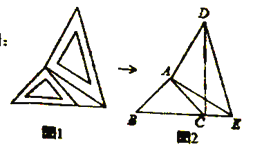
(1)请在图2中找出与![]() 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:![]() .
.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查活动,要求每名学生必选且只能选一项现随机抽查了![]() 名学生,并将其结果绘制成如下不完整的条形统计图和扇形统计图.
名学生,并将其结果绘制成如下不完整的条形统计图和扇形统计图.
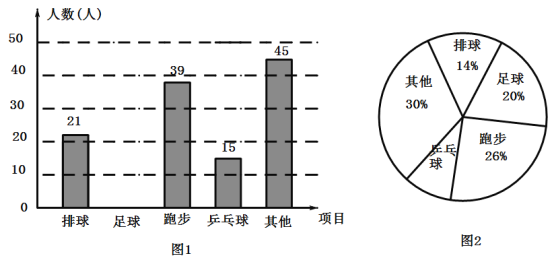 请结合以上信息解答下列问题:
请结合以上信息解答下列问题:
(1)![]() ______;
______;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为______;
(4)已知该校共有3200名学生,请你估计该校最喜爱跑步活动的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的三个顶点坐标如下表:
(1)将下表补充完整,并在直角坐标系中,画出△A′B′C′;
(x,y) | (2x,2y) |
A(2,1) | A′(4,2) |
B(4,3) | B′( ) |
C(5,1) | C′( ) |
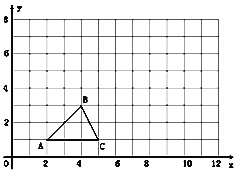
(2)观察两个三角形,可知△ABC∽△A′B′C′两个三角形的是以原点为位似中心的位似三角形,△ABC与△A′B′C′的位似比为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
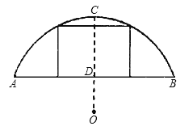
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽为8米(即AB=8米),拱顶高出水面为2米(即CD=2米).
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽6米,船舱顶部为正方形并高出水面1.5米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
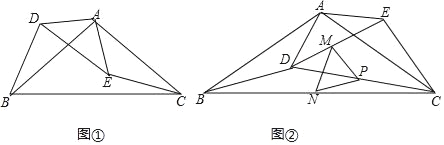
【题目】如图①,在等腰△ABC和△ADE中,AB=AC,AD=AE,且∠BAC=∠DAE=120°.
(1)求证:△ABD≌△ACE;
(2)把△ADE绕点A逆时针方向旋转到图②的位置,连接CD,点M、P、N分别为DE、DC、BC的中点,连接MN、PN、PM,判断△PMN的形状,并说明理由;
(3)在(2)中,把△ADE绕点A在平面内自由旋转,若AD=4,AB=6,请分别求出△PMN周长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点D为
,点D为![]() 的中点,直角
的中点,直角![]() 绕点D旋转,
绕点D旋转,![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于E,F两点,下列结论:①
交于E,F两点,下列结论:①![]() 是等腰直角三角形;②
是等腰直角三角形;②![]() ;③
;③![]() ;④
;④![]() ,其中正确结论是( ).
,其中正确结论是( ).

A.①②④B.②③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2,则y1≤y2,其中正确结论的个数是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
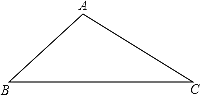
【题目】下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
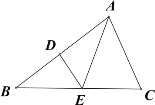
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com