
【题目】某校开展“我最喜爱的一项体育活动”调查活动,要求每名学生必选且只能选一项现随机抽查了![]() 名学生,并将其结果绘制成如下不完整的条形统计图和扇形统计图.
名学生,并将其结果绘制成如下不完整的条形统计图和扇形统计图.
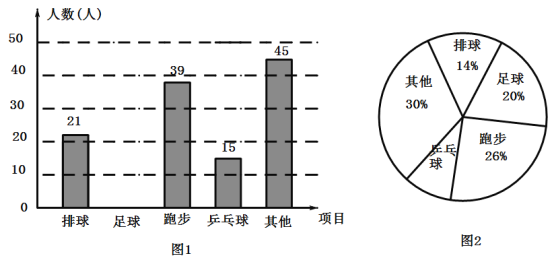 请结合以上信息解答下列问题:
请结合以上信息解答下列问题:
(1)![]() ______;
______;
(2)请补全上面的条形统计图;
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为______;
(4)已知该校共有3200名学生,请你估计该校最喜爱跑步活动的学生人数.
【答案】(1)150;(2)答案见解析;(3)36°;(4)832.
【解析】
(1)根据图中信息列式计算即可;
(2)求得“足球“的人数=150×20%=30人,补全上面的条形统计图即可;
(3)360°×乒乓球”所占的百分比即可得到结论;
(4)根据题意用3200乘以最喜爱跑步活动的学生占比计算即可.
(1)m=21÷14%=150,
故答案为:150;
(2)“足球“的人数=150×20%=30人,
补全上面的条形统计图如图所示;
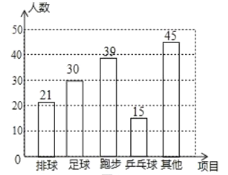
(3)在图2中,“乒乓球”所对应扇形的圆心角的度数为360°×![]() =36°
=36°
故答案为:36°;
(4)3200×26%=832人,
答:估计该校约有832名学生最喜爱跑步活动.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
【题目】如图1,在等腰Rt△ABC中,∠BAC=90°,点E在AC上(且不与点A、C重合).在△ABC的外部作等腰Rt△CED,使∠CED=90°,连接AD,分别以AB,AD为邻边作平行四边形ABFD,连接AF.
(1)求证:△AEF是等腰直角三角形;
(2)如图2,将△CED绕点C逆时针旋转,当点E在线段BC上时,连接AE,求证:AF=![]() AE;
AE;
(3)如图3,将△CED绕点C继续逆时针旋转,当平行四边形ABFD为菱形,且△CED在△ABC的下方时,若AB=2![]() ,CE=2,求线段AE的长.
,CE=2,求线段AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,按以下步骤作图:①分别以 B,C 为圆心,以大于![]() BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
BC 的长为半径作弧,两弧相交于两点 M,N;②作直线 MN 交 AB 于点 D,连接 CD.若 CD=AC,∠A=50°,则∠ACB 的度数为
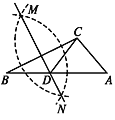
A.90°B.95°C.105°D.110°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某教育局组织了“落实十九大精神,立足岗位见行动”教师演讲比赛,根据各校初赛成绩在小学组、中学组分别选出10名教师参加决赛,这些选手的决赛成绩如图所示:
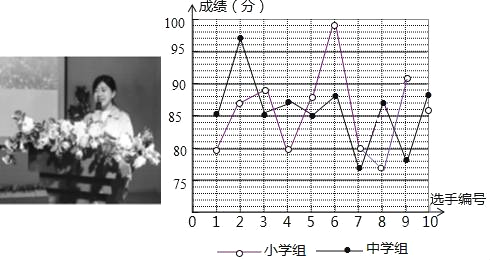
根据上图提供的信息,回答下列问题:
(1)请你把下面表格填写完整:
团体成绩 | 众数 | 平均数 | 方差 |
小学组 |
| 85.7 | 39.6 |
中学组 | 85 |
| 27.8 |
(2)考虑平均数与方差,你认为哪个组的团体成绩更好些,并说明理由;
(3)若在每组的决赛选手中分别选出3人参加总决赛,你认为哪个组获胜的可能性大些?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是BC边上一动点,点E,F分别在AB,AC边上,连接AD,DE,DF,且∠ADE=∠ADF=60°.
小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE=AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:利用AD是∠EDF的角平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证.
想法2:利用AD是∠EDF的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法3:将△ACD绕点A顺时针旋转至△ABG,使得AC和AB重合,然后通过全等三角形的相关知识获证.
请你参考上面的想法,帮助小明证明AE=AF.(一种方法即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 、
、![]() 、
、![]() 在同一条直线上,连结
在同一条直线上,连结![]() .
.
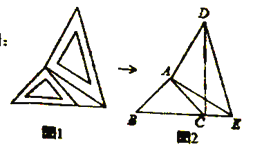
(1)请在图2中找出与![]() 全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
全等的三角形,并给予证明(说明:结论中不得含有未标识的字母);
(2)证明:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com