
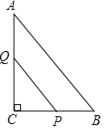
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
【答案】2
【解析】
连接AD,根据PQ∥AB可知∠ADQ=∠DAB,再由点D在∠BAC的平分线上,得出∠DAQ=∠DAB,故∠ADQ=∠DAQ,AQ=DQ.在Rt△CPQ中根据勾股定理可知,AQ=12-4x,故可得出x的值,进而得出结论.
连接AD,
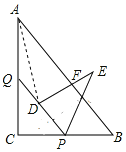
∵PQ∥AB,
∴∠ADQ=∠DAB,
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ,
在Rt△ABC中,∵AB=5,BC=3,
∴AC=4,
∵PQ∥AB,
∴△CPQ∽△CBA,
∴CP:CQ=BC:AC=3:4,设PC=3x,CQ=4x,
在Rt△CPQ中,PQ=5x,
∵PD=PC=3x,
∴DQ=2x,
∵AQ=4-4x,
∴4-4x=2x,解得x=![]() ,
,
∴CP=3x=2;
故答案为:2.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
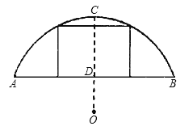
【题目】如图所示,某地有一座圆弧形的拱桥,桥下水面宽为8米(即AB=8米),拱顶高出水面为2米(即CD=2米).
(1)求这座拱桥所在圆的半径.
(2)现有一艘宽6米,船舱顶部为正方形并高出水面1.5米的货船要经过这里,此时货船能顺利通过这座拱桥吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
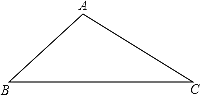
【题目】下面是小东设计的“作△ABC中BC边上的高线”的尺规作图过程.
已知:△ABC.
求作:△ABC中BC边上的高线AD.
作法:如图,
①以点B为圆心,BA的长为半径作弧,以点C为圆心,CA的长为半径作弧,两弧在BC下方交于点E;
②连接AE交BC于点D.
所以线段AD是△ABC中BC边上的高线.
根据小东设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵ =BA, =CA,
∴点B,C分别在线段AE的垂直平分线上( )(填推理的依据).
∴BC垂直平分线段AE.
∴线段AD是△ABC中BC边上的高线.
查看答案和解析>>
科目:初中数学 来源: 题型:
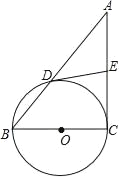
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校计划组织师生共310人参加一次野外研学活动,如果租用6辆大客车和5辆小客车恰好全部坐满.已知每辆大客车的乘客座位数比小客车多15个.
(1)求每辆大客车和每辆小客车的乘客座位数;
(2)由于最后参加活动的人数增加了20人,学校决定调整租车方案,在保持租用车辆总数不变的情况下,为将所有参加活动的师生装载完成,求租用小客车数量的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
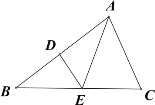
【题目】如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,∠B=30°,∠BAC=80°,且BC+AC=12cm,①求∠CAE的度数;②求△AEC的周长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣(x﹣h)2(h为常数),当自变量x的值满足2≤x≤5时,与其对应的函数值y的最大值为﹣1,则h的值为( )
A. 3或6 B. 1或6 C. 1或3 D. 4或6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com