
【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于点D,DE交AC于点E,且∠A=∠ADE.
(1)求证:DE是⊙O的切线;
(2)若AD=16,DE=10,求BC的长.
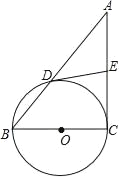
【答案】(1)证明见解析;(2)15.
【解析】
(1)先连接OD,根据圆周角定理求出∠ADB=90°,根据直角三角形斜边上中线性质求出DE=BE,推出∠EDB=∠EBD,∠ODB=∠OBD,即可求出∠ODE=90°,根据切线的判定推出即可.
(2)首先证明AC=2DE=20,在Rt△ADC中,DC=12,设BD=x,在Rt△BDC中,BC2=x2+122,在Rt△ABC中,BC2=(x+16)2-202,可得x2+122=(x+16)2-202,解方程即可解决问题.
(1)证明:连结OD,∵∠ACB=90°,
∴∠A+∠B=90°,
又∵OD=OB,
∴∠B=∠BDO,
∵∠ADE=∠A,
∴∠ADE+∠BDO=90°,
∴∠ODE=90°.
∴DE是⊙O的切线;
(2)连结CD,∵∠ADE=∠A,
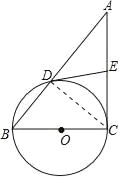
∴AE=DE.
∵BC是⊙O的直径,∠ACB=90°.
∴EC是⊙O的切线.
∴DE=EC.
∴AE=EC,
又∵DE=10,
∴AC=2DE=20,
在Rt△ADC中,DC=![]()
设BD=x,在Rt△BDC中,BC2=x2+122,
在Rt△ABC中,BC2=(x+16)2﹣202,
∴x2+122=(x+16)2﹣202,解得x=9,
∴BC=![]() .
.


 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,
(1)求点B的坐标;
(2)当点P运动什么位置时,使得∠CPD =∠OAB,且![]() ,求这时点P的坐标;
,求这时点P的坐标;
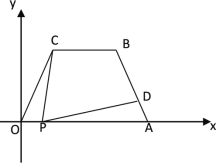
(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为线段
为线段![]() 上一动点(不与点
上一动点(不与点![]() ,
,![]() 重合),在
重合),在![]() 同侧分别作正三角形
同侧分别作正三角形![]() 和等边三角形
和等边三角形![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() ,以下结论一定正确的有( )个
,以下结论一定正确的有( )个
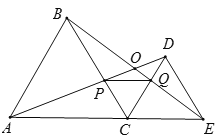
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]()
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
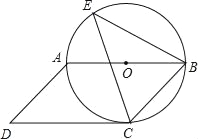
【题目】如图,四边形ABCD是平行四边形,以边AB为直径的⊙O经过点C,E是⊙O上的一点,且∠BEC=45°.
(1)试判断CD与⊙O的位置关系,并说明理由;
(2)若BE=8cm,sin∠BCE=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 是
是![]() 的两条高线,且它们相交于
的两条高线,且它们相交于![]() 是
是![]() 边的中点,连结
边的中点,连结![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,已知
,已知![]() .
.
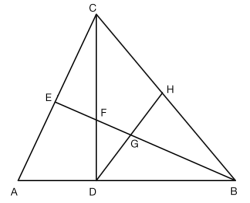
(1)求证BF=AC.
(2)若BE平分![]() .
.
①求证:DF=DG.
②若AC=8,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
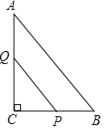
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一座钢结构桥梁的框架是△ABC,水平横梁BC长18米,中柱AD高6米,其中D是BC的中点,且AD⊥BC.
(1)求sinB的值;
(2)现需要加装支架DE、EF,其中点E在AB上,BE=2AE,且EF⊥BC,垂足为点F,求支架DE的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com