
【题目】如图,![]() 中,
中,![]() 是高,点
是高,点![]() 是
是![]() 上一点,
上一点,![]() ,
,![]() ,
,![]() 分别是
分别是![]() 上的点,且
上的点,且![]() .
.
(1)求证:![]() .
.
(2)探索![]() 和
和![]() 的关系,并证明你的结论.
的关系,并证明你的结论.
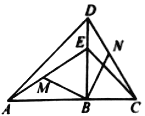
【答案】(1)证明见解析;(2)BM=BN,MB⊥BN;证明见解析.
【解析】
(1)由已知的等量关系利用SAS即可证明△ABE≌△DBC;
(2)利用(1)的全等得到∠BAM=∠BDN.,再根据![]() ,
,![]() ,证明△ABM≌△DBN得到BM=BN,∠ABM=∠DBN.再利用同角的余角相等即可得到MB⊥MN.
,证明△ABM≌△DBN得到BM=BN,∠ABM=∠DBN.再利用同角的余角相等即可得到MB⊥MN.
(1)证明:∵DB是高,∴∠ABE=∠DBC=90°.
在△ABE 和△DBC中,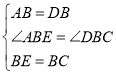 ,
,
∴△ABE≌△DBC.
(2)解:BM=BN,MB⊥MN,证明如下:
∵△ABE≌△DBC,∴∠BAM=∠BDN.
在△ABM 和△DBN 中,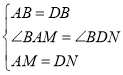
∴△ABM≌△DBN.
∴BM=BN, ∠ABM=∠DBN.
∴∠BDN+∠DBM=∠ABM+∠DBM=∠ABD=90°.
∴MB⊥BN.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
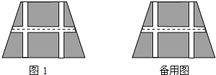
【题目】如图,要设计一个等腰梯形的花坛,花坛上底![]() 米,下底
米,下底![]() 米,上下底相距
米,上下底相距![]() 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为![]() 米.
米.
![]() 用含
用含![]() 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
![]() 当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
![]() 根据设计的要求,甬道的宽不能超过
根据设计的要求,甬道的宽不能超过![]() 米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是
米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是![]() ,花坛其余部分的绿化费用为每平方米
,花坛其余部分的绿化费用为每平方米![]() 万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
科目:初中数学 来源: 题型:
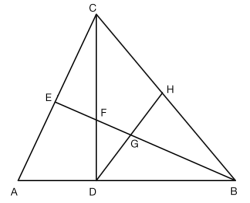
【题目】如图,![]() 是
是![]() 的两条高线,且它们相交于
的两条高线,且它们相交于![]() 是
是![]() 边的中点,连结
边的中点,连结![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,已知
,已知![]() .
.
(1)求证BF=AC.
(2)若BE平分![]() .
.
①求证:DF=DG.
②若AC=8,求BG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
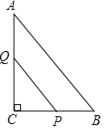
【题目】如图,在Rt△ABC中,∠C=90°,AB=5,BC=3,点P、Q分别在边BC、AC上,PQ∥AB,把△PCQ绕点P旋转得到△PDE(点C、Q分别与点D、E对应),点D落在线段PQ上,若AD平分∠BAC,则CP的长为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
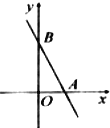
【题目】如图,在平面直角坐标系中,直线![]() 分别交
分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() 点,
点,![]() ,且
,且![]() 满足
满足![]() ,点
,点![]() 在直线
在直线![]() 的左侧,且
的左侧,且![]() .
.
(1)求![]() 的值;
的值;
(2)若点![]() 在
在![]() 轴上,求点
轴上,求点![]() 的坐标;
的坐标;
(3)若![]() 为直角三角形,求点
为直角三角形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】全面两孩政策实施后,甲,乙两个家庭有了各自的规划.假定生男生女的概率相同,回答下列问题:
(1)甲家庭已有一个男孩,准备再生一个孩子,则第二个孩子是女孩的概率是 ;
(2)乙家庭没有孩子,准备生两个孩子,求至少有一个孩子是女孩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
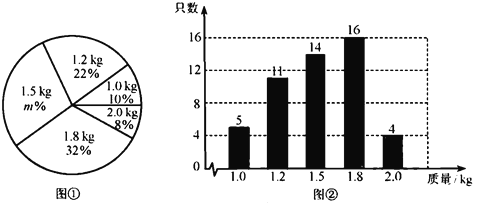
(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com