
【题目】如图,边长为24的等边三角形ABC中,M是高CH所在直线上的一个动点,连结MB,将线段BM绕点B逆时针旋转60°得到BN,连结HN.则在点M运动过程中,线段HN长度的最小值是( )

A. 12B. 6C. 3D. 1
【答案】B
【解析】
取CB的中点G,连接MG,根据等边三角形的性质可得BD=BG,再求出∠HBN=∠MBG,根据旋转的性质可得MB=NB,然后利用“边角边”证明△MBG≌△NBH,再根据全等三角形对应边相等可得HN=MG,然后根据垂线段最短可得MG⊥CH时最短,再根据∠BCH=30°求解即可.
如图,取BC的中点G,连接MG,
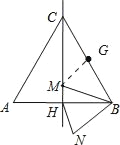
∵旋转角为60°,
∴∠MBH+∠HBN=60°,
又∵∠MBH+∠MBC=∠ABC=60°,
∴∠HBN=∠GBM,
∵CH是等边△ABC的对称轴,
∴HB=![]() AB,
AB,
∴HB=BG,
又∵MB旋转到BN,
∴BM=BN,
在△MBG和△NBH中,
 ,
,
∴△MBG≌△NBH(SAS),
∴MG=NH,
根据垂线段最短,当MG⊥CH时,MG最短,即HN最短,
此时∠BCH=![]() ×60°=30°,CG=
×60°=30°,CG=![]() AB=
AB=![]() ×24=12,
×24=12,
∴MG=![]() CG=
CG=![]() ×12=6,
×12=6,
∴HN=6,
故选B.


科目:初中数学 来源: 题型:
【题目】元旦放假期间,小明和小华准备到西安的大雁塔(记为A)、白鹿原(记为B)、兴庆公园(记为C)、秦岭国家植物园(记为D)中的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点被选中的可能性相同
(1)求小明选择去白鹿原游玩的概率;
(2)用树状图或列表的方法求小明和小华选择去同一个地方游玩的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC是等边三角形,点D是BC边上一动点,点E,F分别在AB,AC边上,连接AD,DE,DF,且∠ADE=∠ADF=60°.
小明通过观察、实验,提出猜想:在点D运动的过程中,始终有AE=AF,小明把这个猜想与同学们进行交流,通过讨论,形成了证明该猜想的几种想法:
想法1:利用AD是∠EDF的角平分线,构造△ADF的全等三角形,然后通过等腰三角形的相关知识获证.
想法2:利用AD是∠EDF的角平分线,构造角平分线的性质定理的基本图形,然后通过全等三角形的相关知识获证.
想法3:将△ACD绕点A顺时针旋转至△ABG,使得AC和AB重合,然后通过全等三角形的相关知识获证.
请你参考上面的想法,帮助小明证明AE=AF.(一种方法即可)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 的坐标为(3,4),
的坐标为(3,4),![]() 轴于点
轴于点![]() ,
,![]() 是线段
是线段![]() 上一点,且
上一点,且![]() ,点
,点![]() 从原点
从原点![]() 出发,沿
出发,沿![]() 轴正方向运动,
轴正方向运动,![]() 与直线
与直线![]() 交于
交于![]() ,则
,则![]() 的面积( )
的面积( )
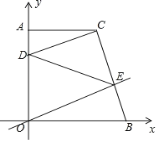
A.逐渐变大B.先变大后变小C.逐渐变小D.始终不变
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地在城区美化工程招标时,有甲、乙两个工程队投标.经测算,获得以下信息:
信息1:乙队单独完成这项工程需要60天;
信息2:若先由甲、乙两队合做16天,剩下的工程再由乙队单独做20天可以完成;
信息3:甲队施工一天需付工程款3.5万元,乙队施工一天需付工程款2万元.
根据以上信息,解答下列问题:
(1)甲队单独完成这项工程需要多少天?
(2)若该工程计划在50天内完成,在不超过计划天数的前提下,是由甲队或乙队单独完成该工程省钱?还是由甲、乙两队全程合作完成该工程省钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标中,四边形OABC是梯形,且AB = OC = 4,CB∥OA,OA = 7,∠COA = 60°,点P为x轴上的—个动点,点P不与点0、点A重合.连结CP,过点P作PD交AB于点D,
(1)求点B的坐标;
(2)当点P运动什么位置时,使得∠CPD =∠OAB,且![]() ,求这时点P的坐标;
,求这时点P的坐标;
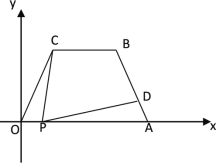
(3)当点P运动什么位置时,△OCP为等腰三角形,直接写出这时点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,要设计一个等腰梯形的花坛,花坛上底![]() 米,下底
米,下底![]() 米,上下底相距
米,上下底相距![]() 米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为
米,在两腰中点连线(虚线)处有一条横向甬道,上下底之间有两条纵向甬道,各甬道的宽度相等.设甬道的宽为![]() 米.
米.
![]() 用含
用含![]() 的式子表示横向甬道的面积;
的式子表示横向甬道的面积;
![]() 当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
![]() 根据设计的要求,甬道的宽不能超过
根据设计的要求,甬道的宽不能超过![]() 米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是
米.如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是![]() ,花坛其余部分的绿化费用为每平方米
,花坛其余部分的绿化费用为每平方米![]() 万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?
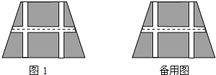
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程队承包了某标段全长1800米的过江隧道施工任务,甲、乙两个班组分别从东、西两端同时掘进.已知甲组比乙组平均每天多掘进2米,经过5天施工,两组共掘进了60米.
(1)求甲、乙两班组平均每天各掘进多少米?
(2)为加快工程进度,通过改进施工技术,在剩余的工程中,甲组平均每天能比原来多掘进2米,乙组平均每天能比原来多掘进1米.按此施工进度,能够比原来少用多少天完成任务?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com