[题目]计算:(1)-4-1-(-2)0+3÷,(2)(π-3)0+()-2+4×2-1,(3)()-1+(π-2018)0-(-1)2019. 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】计算：

(1)－4－1－(－2)0＋3÷；

(2)(π－3)0＋()－2＋4×2－1；

(3)()－1＋(π－2018)0－(－1)2019.

【答案】(1) －;(2)7;(3)4

【解析】

（1）第一项按负整数指数幂的性质运算，第二项按零指数幂运算，第三项先按负整数指数幂的性质运算再计算除法，最后再算加减即可；

（2）第一项按按零指数幂运算法则计算，，第二项按负整数指数幂的性质运算，第三项先按负整数指数幂的性质运算再计算乘法，最后再算加法即可；

（3）第一项按负整数指数幂的性质运算，第二项按零指数幂运算，第三项按负整数指数幂的性质运算，最后再算加减即可.

(1)原式＝－－1＋3÷9＝－－1＋＝－.

(2)原式＝1＋4＋4×＝7.

(3)原式＝2＋1－(－1)＝4.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】有以下三角形：①三角形三边之比为2：3：2；②三角形的三边为3，4，5；③三角形三个角分别为20°，70°，90°；④三角形三个角的比为1：2：3．其中不是直角三角形的个数是（　　）

A. 1个 B. 2个 C. 3个 D. 4

查看答案和解析>>

科目：初中数学 来源： 题型：

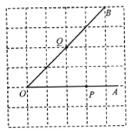
【题目】如图，点P，Q分别是∠AOB的边OA，OB上的点.

(1)过点P画OB的垂线，垂足为H；

(2)过点Q画OA的垂线，交OA于点C，连接PQ；

(3)线段QC的长度是点Q到的距离，的长度是点P到直线OB的距离，因为直线外一点和直线上各点连接的所有线段中，垂线段最短，所以线段PQ、PH的大小关系是 (用“＜”号连接).

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在等腰△ABC中，CA=CB，AD是腰BC边上的高，△ACD的内切圆⊙E分别与边AD、BC相切于点F、G，连AE、BE．
（1）求证：AF=BG；
（2）过E点作EH⊥AB于H，试探索线段EH与线段AB的数量关系，并说明理由．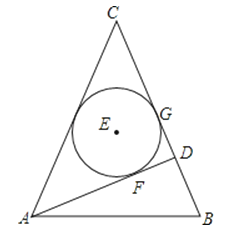

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】P是⊙O外一点，PA、PB分别与⊙O相切于点A、B，点C是劣弧AB上任意一点，经过点C作⊙O的切线，分别交PA、PB于点D、E．若PA=4，则△PDE的周长是（　　）
A.4
B.8
C.12
D.不能确定

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，在数轴上，点A表示-5，点B表示10.动点P从点A出发，沿数轴正方向以每秒1个单位的速度匀速运动;同时，动点Q从点B出发，沿数轴负方向以每秒2个单位的速度匀速运动.设运动时间为t秒.

(1)当t为秒时，P，Q两点相遇，求出相遇点所对应的数;

(2)当t为何值时，P，Q两点的距离为3个单位长度，并求出此时点P对应的数.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】为发展校园足球运动，某县城区四校决定联合购买一批足球运动装备，市场调查发现：甲、乙两商场以同样的价格出售同种品牌的足球队服和足球，已知每套队服比每个足球多50元，两套队服与三个足球的费用相等，经洽谈，甲商场优惠方案是：每购买十套队服，送一个足球；乙商场优惠方案是：若购买队服超过80套，则购买足球打八折．

（1）求每套队服和每个足球的价格是多少？

（2）若城区四校联合购买100套队服和a个足球，请用含a的式子分别表示出到甲商场和乙商场购买装备所花的费用；

（3）假如你是本次购买任务的负责人，你认为到哪家商场购买比较合算？

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两人相约周末登花果山，甲、乙两人距地面的高度y（米）与登山时间x（分）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：

（1）甲登山上升的速度是每分钟　　米，乙在A地时距地面的高度b为　　米．

（2）若乙提速后，乙的登山上升速度是甲登山上升速度的3倍，请求出乙登山全程中，距地面的高度y（米）与登山时间x（分）之间的函数关系式．

（3）登山多长时间时，甲、乙两人距地面的高度差为50米？