
【题目】在边长为12的正方形![]() 中,对角线
中,对角线![]() 、
、![]() 交于点
交于点![]() ,点
,点![]() 、
、![]() 分别为
分别为![]() 、
、![]() 边上的动点,且始终保持
边上的动点,且始终保持![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
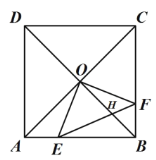
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值;
的值;
(3)在运动的过程中,![]() 是否存在最大值?若存在,请求出
是否存在最大值?若存在,请求出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 存在最大值为18.
存在最大值为18.
【解析】
(1)由正方形的性质可得OA=OB,∠OAE=∠OBF,再结合OE⊥OF可证明![]() ,进而证明△AOE≌△BOF;
,进而证明△AOE≌△BOF;
(2)根据(1)得AE=BF,由勾股定理求得EF的值,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,得
,得![]() ,故
,故![]() ,求出EH和FH的值,即可得出结论;
,求出EH和FH的值,即可得出结论;
(3)证明![]() ,得
,得![]() ,设
,设![]() ,则
,则![]() ,得
,得![]() ,故可求解.
,故可求解.
(1)∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
(2)由(1)知,![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
设![]() ,则
,则![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.

(3)由(1)知,![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,
,
∴![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,
则![]() ,
,
即当![]() 时,
时,![]() 有最大值为18,
有最大值为18,
即![]() 存在最大值为18.
存在最大值为18.


科目:初中数学 来源: 题型:
【题目】将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:
(1)填空:AP= cm,PF= cm.
(2)求出容器中牛奶的高度CF.
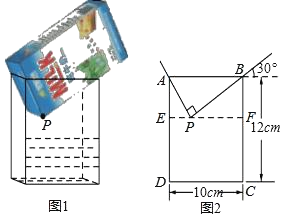
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与
与![]() 轴交于点A和点B(3,0),与
轴交于点A和点B(3,0),与![]() 轴交于点C(0,3),P是线段BC上一点,过点P作PN∥
轴交于点C(0,3),P是线段BC上一点,过点P作PN∥![]() 轴交
轴交![]() 轴于点N,交抛物线于点M.
轴于点N,交抛物线于点M.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为2,点Q是第一象限抛物线上的一点,且△QMC和△PMC的面积相等,求点Q的坐标;
(3)如果![]() ,求tan∠CMN的值.
,求tan∠CMN的值.
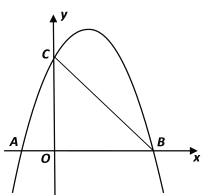
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AC=4,AB=2,将矩形ABCD绕点A旋转得到矩形AB'C'D',使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C'上取点F,使B'F=AB.
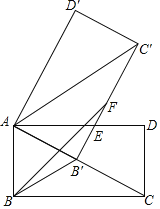
(1)求证:AE=C'E;
(2)求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
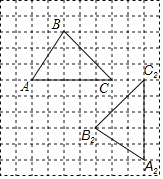
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,△ABC为格点三角形(顶点在网格线的交点).
(1)将△ABC向上平移2个单位得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕着某点O逆时针方向旋转90°后,得到△A2B2C2,请画出旋转中心O,并直接写出在此旋转过程中,线段AB扫过的区域的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学兴趣小组活动中,李燕和刘凯两位同学设计了如图所示的两个转盘做游戏(每个转盘被分成面积相等的几个扇形,并在每个扇形区域内标上数字).游戏规则如下:两人分别同时转动甲、乙转盘,转盘停止后,若指针所指区域内两数和小于12,则李燕获胜;若指针所指区域内两数和等于12,则为平局;若指针所指区域内两数和大于12,则刘凯获胜(若指针停在等分线上,重转一次,直到指针指向某一份内为止).

(1)请用列表的方法表示出上述游戏中两数和的所有可能的结果;
(2)分别求出李燕和刘凯获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
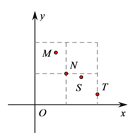
【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中![]() 四位同学的单词记忆效率
四位同学的单词记忆效率![]() 与复习的单词个数
与复习的单词个数![]() 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,其中AB=4,∠AOC=120°,P为⊙O上的动点,连AP,取AP中点Q,连CQ,则线段CQ的最大值为( )

A. 3 B. 1+![]() C. 1+3
C. 1+3![]() D. 1+
D. 1+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为45°,为了方便行人安全过天桥,市政部门决定降低坡度.使新坡面的倾斜角为30°.若新坡脚前需留2.5米的人行道,问离原坡脚C点10米的建筑物是否需要拆除?请说明理由.(参考数据![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com