
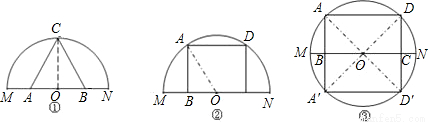
(1)在图①的半径为R的半圆O内(含弧),求出一边落在直径MN上的最大的正三角形的面积?
(2)在图②的半径为R的半圆O内(含弧),求出一边落在直径MN上的最大的正方形的面积?
问题解决
(3)如图③,现有一块半径R=6的半圆形钢板,是否可以裁出一边落在MN上的面积最大的矩形?若存在,请说明理由,并求出这个矩形的面积;若不存在,说明理由?

(1)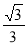 R2;(2)
R2;(2)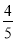 R2;(3)存在,36.
R2;(3)存在,36.
【解析】
试题分析:(1)如图①,△ACB为满足条件的面积最大的正三角形.连接OC,则OC⊥AB,根据垂径定理得到AB=2OB,然后利用含30°的直角三角形三边的关系求出OB,再利用三角形的面积公式计算即可;
(2)如图②,正方形ABCD为满足条件的面积最大的正方形.连接OA.令OB=a,则AB=2a,利用勾股定理求出边长,再利用正方形的面积公式计算即可;
(3)如图③,先作一边落在直径MN上的矩形ABCD,使点A、D在弧MN上,再作半圆O及矩形ABCD关于直径MN所在直线的对称图形,A、D的对称点分别是A′、D′.连接A′D、OD,则A′D为⊙O的直径.在Rt△AA′D中,当OA⊥A′D时,S△AA′D的面积最大.
(1)如图①,△ACB为满足条件的面积最大的正三角形.
连接OC,则OC⊥AB.
∵AB=2OB•tan30°=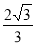 R,
R,
∴S△ACB=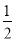 AB•OC=
AB•OC=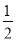 ×
×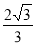 R•R=
R•R=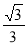 R2.
R2.
(2)如图②,正方形ABCD为满足条件的面积最大的正方形.
连接OA.令OB=a,则AB=2a.
在Rt△ABO中,a2+(2a)2=R2.
即a2=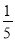 R2.
R2.
S正方形ABCD=(2a)2=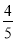 R2.
R2.
(3)存在.
如图③,先作一边落在直径MN上的矩形ABCD,使点A、D在弧MN上,再作半圆O及矩形ABCD关于直径MN
所在直线的对称图形,A、D的对称点分别是A′、D′.
连接A′D、OD,则A′D为⊙O的直径.
∴S矩形ABCD=AB•AD=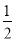 AA′•AD=S△AA′D
AA′•AD=S△AA′D
∵在Rt△AA′D中,当OA⊥A′D时,S△AA′D的面积最大.
∴S矩形ABCD最大=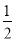 •2R•R=R2=36.
•2R•R=R2=36.
考点: 1.垂径定理;2.等边三角形的性质;3.勾股定理;4.正方形的性质.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源:2013-2014学年江苏省无锡市锡山区九年级下学期期中考试(一模)数学试卷(解析版) 题型:填空题
为考察甲、乙两种小麦的长势,分别从中抽取50株小麦,测得苗高,经过数据处理,它们的平均数相同,方差分别为甲的方差 ,乙的方差
,乙的方差 ,由此可以估计 种小麦长的比较整齐.
,由此可以估计 种小麦长的比较整齐.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:解答题
如图1,已知有一张三角形纸片ABC的一边AB=10,若D为AB边上的点,过点D作DE∥BC交AC于点E,分别过点D、E作DF⊥BC于F,EG⊥BC于G,把三角形纸片ABC分别沿DE、DF、EG按图1方式折叠,点A、B、C分别落在A′、B′、C′处.若点A′、B′、C′在矩形DFGE内或者其边上,且互不重合,此时我们称△A′B′C′(即图中阴影部分)为“重叠三角形”.
实践探究:
(1)当AD=4时,
①若∠A=90°,AB=AC,请在图2中画出“重叠三角形”,S△A′B′C′= ;
②若AB=AC,BC=12,如图3,S△A′B′C′= ;
③若∠B=30°,∠C=45°,如图4,S△A′B′C′= .
(2)若△ABC为等边三角形(如图5),AD=m,且重叠三角形A′B′C′存在,试用含m的代数式表示重叠三角形A′B′C′ 的面积,并写出m的取值范围.

查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市九年级4月高效课堂调研数学试卷(解析版) 题型:选择题
已知一组数据:15,13,15,16,17,16,14,15,则这组数据的极差与众数分别是( )
A.4,15 B.3,15 C.4,16 D.3,16
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:解答题
在一个不透明的口袋里装有只有颜色不同的黑、白两种颜色的球共20个,某学习小组做摸球实验,将球搅匀后从中随机摸出一个球记下颜色,然后把它放回袋中,不断重复。下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到白球的次数m | 58 | 96 | 116 | 295 | 484 | 601 |
摸到白球的频率 | 0.58 | 0.64 | 0.58 | 0.59 | 0.605 | 0.601 |
请估计:当n很大时,摸到白球的频率将会接近_________;
假如你去摸一次,你摸到白球的概率是________;摸到黑球的概率是_____;
试估计口袋中黑、白两种颜色的球各有多少个?
解决了上面的问题,小明同学猛然顿悟,过去一个悬而未决的问题有办法了。这个问题是:在一个不透明的口袋里装有若干个白球,在不允许将球倒出来数的情况下,如何估计白球的个数(可以借助其他工具及用品)?请你应用统计与概率的思想和方法解决这个问题,写出解决这个问题的主要步骤及估算方法。
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市新区九年级第一次模拟考试数学试卷(解析版) 题型:填空题
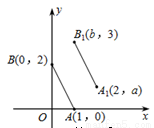
如图 ,A、B的坐标分别为(1,0)、(0,2),若将线段AB平移到至A B
B , A
, A 、B
、B 的坐标分别为(2,a)、(b,3),则a+b= .
的坐标分别为(2,a)、(b,3),则a+b= .
查看答案和解析>>
科目:初中数学 来源:2013-2014学年江苏省无锡市崇安区九年级下学期期中统考(一模)数学试卷(解析版) 题型:解答题
如图,二次函数y=ax2+2ax+b的图象与x轴交于点A、B,与y轴交于点C(0,),其顶点在直线y=-2x上.
(1)求a,b的值;
(2)写出当-2≤x≤2时,二次函数y的取值范围;
(3)以AC、CB为一组邻边作□ACBD,则点D关于x轴的对称点D’是否在该二次函数的图象上?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com