
����Ŀ��Ϊ�����������˾ӳ�������ƽԭ��ί�ظ�����Ҫ·��·�Ƹ���Ϊ����·�ƣ���֪����·���ۼ�Ϊ5000Ԫ/����Ŀǰ�����̼��д˲�Ʒ�����̼������·���������������·�Ʋ�����100������ԭ�۸����һ�ι���100�����ϣ��ҹ���ĸ���ÿ����һ������۸����10Ԫ��������·�Ƶ��ۼ۲��õ���3500Ԫ/�����ҵ�һ�ɰ�ԭ�۵�80�G���ۣ��ֹ������·��x�������ȫ���ڼ��̼ҹ�����������Ϊy1Ԫ�����ȫ�������̼ҹ�����������Ϊy2Ԫ.
��1���ֱ����y1��y2��x֮��ĺ�����ϵʽ��
��2������ί�ظ�Ͷ��140��Ԫ������ܹ�����ٸ�����·�ƣ�
���𰸡���1��y1=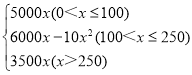 ��y2=5000��80%x=4000x����2������ܹ���400��·�ƣ�
��y2=5000��80%x=4000x����2������ܹ���400��·�ƣ�
��������
�����������1���Լף����ڹ��������ͬ���ۼ�Ҳ��ͬ������谴��������ֳ������ɵ�����ϵ��������=�ۼ�������������г�������ϵʽ��
���ң���������ϵ��������=�ۼ�������������г�������ϵʽ��
��2���ֱ����Ͷ�ʶ��ڼ����̼Ҹ��ܹ����̫����·�Ƶ��������Ƚϵó����ֵ��
�����������1���������֪��
��0��x��100ʱ������һ����5000Ԫ����y1=5000x��
��x��100ʱ��
���������ÿ����һ������۸����10Ԫ�����ۼ۲��õ���3500Ԫ/����
��x��![]() +100=250����
+100=250����
��100��x��250ʱ������һ����5000-10��x-100��Ԫ��
��y1=-10x2+6000x��
��x��250ʱ������һ����3500Ԫ��
��y1=3500x��
��y1=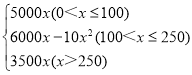 ��
��
y2=5000��80%x=4000x��
��2���ڼ��̼ң���0��x��100ʱ��y1=5000x��500000��1400000��
��100��x��250ʱ��y1=6000x-10x2=-10��x-300��2+900000��1400000��
����3500x=1400000����x=400��
�����̼ң���4000x=1400000��
��x=350����
��ѡ����̼ң�����ܹ���400��·�ƣ�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
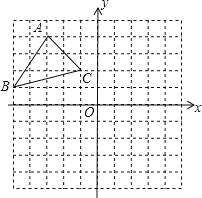
����Ŀ����ͼ������ֽ��ÿ��С�����εı߳����ǵ�λ1����ABC���������㶼�ڸ���ϣ����������ƽ��ֱ������ϵ����������⣺
��1������ABC����ƽ��3����λ����������ƽ��2����λ���ȣ���������ƽ�ƺ�ġ�A1B1C1��
��2��д��A1��C1�����ꣻ
��3������A1B1C1��C1��ʱ����ת90�㣬������ת��ġ�A2B2C1�����߶�B1C1��ת������ɨ�����������������У���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x�ķ���2x + m = 5�Ľ���x =��1����m��ֵΪ�� ��
A. 3 B. 7 C. ��7 D. ��3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������X��Y����һ�������㡰*����X*Y=aX+bY������a��bΪ��������ʽ�ұ���ͨ���ļӷ��ͳ˷�������.��֪��3*5=15��4*7=28����ô2*3=__________ ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������������෴���Ļ��� ��
A�����űض�Ϊ�� B�����űض�Ϊ�� C��һ���������� D��һ����С����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�߶�a=4��b=16���߶�c��a��b�ı��������ôc���ڣ� ��
A.10
B.8
C.��8
D.��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ʹ�ú���ֵΪ����Ա�����ֵ��Ϊ��������㡣���磬���ں���![]() ����
����![]() =0���ɵ�
=0���ɵ�![]() =1�����Ǿ�˵1�Ǻ���
=1�����Ǿ�˵1�Ǻ���![]() ����㡣 ��֪����
����㡣 ��֪����![]() (
(![]() ����)��
����)��
��1����![]() =0ʱ����ú�������㣻
=0ʱ����ú�������㣻
��2��֤��������![]() ȡ��ֵ���ú�������������㣻
ȡ��ֵ���ú�������������㣻
��3���躯�����������ֱ�Ϊ![]() ��
��![]() ����
����![]() ����ʱ����ͼ����
����ʱ����ͼ����![]() ��Ľ���ֱ�ΪA��B(��A�ڵ�B���)����M��ֱ��
��Ľ���ֱ�ΪA��B(��A�ڵ�B���)����M��ֱ��![]() �ϣ���MA��MB��Сʱ����ֱ��AM�ĺ�������ʽ��
�ϣ���MA��MB��Сʱ����ֱ��AM�ĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����д����ҵı��Σ�������ʽ�ֽ����( )
A. (x + 3)(x��2)=x2+x��6 B. ax��ay��1=a(x��y)��1
C. 8a2b3=2a24b3 D. x2��4=(x + 2)(x��2)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
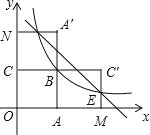
����Ŀ����ͼ���ı���OABC�DZ߳�Ϊ2�������Σ�����y=![]() ��k��0����ͼ����B����������OABC�ֱ���ֱ��AB��BC���ۣ��õ�������MABC�䣬NA��BC�����߶�MC�䣬NA��ֱ��뺯��y=
��k��0����ͼ����B����������OABC�ֱ���ֱ��AB��BC���ۣ��õ�������MABC�䣬NA��BC�����߶�MC�䣬NA��ֱ��뺯��y=![]() ��k��0����ͼ���ڵ�E��F����ֱ��EF��x��Ľ�������Ϊ ��
��k��0����ͼ���ڵ�E��F����ֱ��EF��x��Ľ�������Ϊ ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com