
【题目】使得函数值为零的自变量的值称为函数的零点。例如,对于函数![]() ,令
,令![]() =0,可得
=0,可得![]() =1,我们就说1是函数
=1,我们就说1是函数![]() 的零点。 己知函数
的零点。 己知函数![]() (
(![]() 为常数)。
为常数)。
(1)当![]() =0时,求该函数的零点;
=0时,求该函数的零点;
(2)证明:无论![]() 取何值,该函数总有两个零点;
取何值,该函数总有两个零点;
(3)设函数的两个零点分别为![]() 和
和![]() ,且
,且![]() ,此时函数图象与
,此时函数图象与![]() 轴的交点分别为A、B(点A在点B左侧),点M在直线
轴的交点分别为A、B(点A在点B左侧),点M在直线![]() 上,当MA+MB最小时,求直线AM的函数解析式。
上,当MA+MB最小时,求直线AM的函数解析式。
【答案】(1)![]() 和
和![]() ;(2)证明见解析;(3)AM的解析式为
;(2)证明见解析;(3)AM的解析式为![]()
【解析】
试题分析:(1)根据题中给出的函数的零点的定义,将m=0代入y=x2-2mx-2(m+3),然后令y=0即可解得函数的零点;
(2)令y=0,函数变为一元二次方程,要想证明方程有两个解,只需证明△>0即可;
(3)根据题中条件求出函数解析式进而求得A、B两点坐标,个、作点B关于直线y=x-10的对称点B′,连接AB′,求出点B′的坐标即可求得当MA+MB最小时,直线AM的函数解析式.
试题解析:(1)当![]() =0时,该函数为
=0时,该函数为![]() ,令
,令![]() =0,可得
=0,可得![]() ,
,
∴当![]() =0时,求该函数的零点为
=0时,求该函数的零点为![]() 和
和![]() 。
。
(2)令![]() =0,得△=
=0,得△=![]() ,
,
∴无论![]() 取何值,方程
取何值,方程![]() 总有两个不相等的实数根。
总有两个不相等的实数根。
即无论![]() 取何值,该函数总有两个零点
取何值,该函数总有两个零点
(3)依题意有![]() ,
,![]()
由![]() 得
得![]() ,即
,即![]() ,解得
,解得![]() 。
。
∴函数的解析式为![]() 令
令![]() =0,解得
=0,解得![]() 。
。
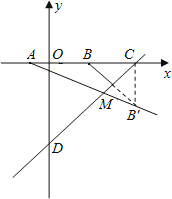
∵点A在点B左侧,∴A(![]() ),B(4,0)。
),B(4,0)。
作点B关于直线![]() 的对称点B’,连结AB’,则AB’与直线
的对称点B’,连结AB’,则AB’与直线![]() 的交点就是满足条件的M点。易求得直线
的交点就是满足条件的M点。易求得直线![]() 与
与![]() 轴、
轴、![]() 轴的交点分别为C(10,0),D(0,10)。
轴的交点分别为C(10,0),D(0,10)。
连结CB’,则∠BCD=45°,∴BC=CB’=6,∠B’CD=∠BCD=45°。
∴∠BCB’=90°,即B’(![]() )。设直线AB’的解析式为
)。设直线AB’的解析式为![]() ,则
,则
![]() ,解得
,解得![]() ∴直线AB’的解析式为
∴直线AB’的解析式为![]() ,
,
即AM的解析式为![]()


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】为增强学生的身体素质,教育行政部门规定每位学生每天参加户外活动的平均时间不少于1小时. 为了解学生参加户外活动的情况,对部分学生参加户外活动的时间进行抽样调查,并将调查结果绘制作成如下两幅不完整的统计图,
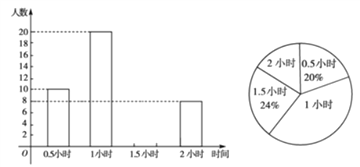
请你根据图中提供的信息解答下列问题:
(1)在这次调查中共调查了多少名学生?
(2)求户外活动时间为1.5小时的人数,并补充频数分布直方图;
(3)户外活动时间的众数和中位数分别是多少?
(4)若该市共有20000名学生,大约有多少学生户外活动的平均时间符合要求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列去括号中,正确的是【 】
A. -(1-2a)=-1-2a B. x2 +(-1-2x)= x2-l +2x
C. 5b-(2c-1)= 5b-2c +1 D. -(m +n)-q =-m-n + q
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为创办“生活宜居城市”,平原县委县府把主要路段路灯更换为节能路灯.已知节能路灯售价为5000元/个,目前两个商家有此产品.甲商家用如下方法促销:若购买路灯不超过100个,按原价付款;若一次购买100个以上,且购买的个数每增加一个,其价格减少10元,但节能路灯的售价不得低于3500元/个.乙店一律按原价的80℅销售.现购买节能路灯x个,如果全部在甲商家购买,则所需金额为y1元;如果全部在乙商家购买,则所需金额为y2元.
(1)分别求出y1、y2与x之间的函数关系式;
(2)若县委县府投资140万元,最多能购买多少个节能路灯?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场用36000元购进甲、乙两种商品,销售完后共获利6000元.其中甲种商品每件进价120元,售价138元;乙种商品每件进价100元,售价120元.
(1)该商场购进甲、乙两种商品各多少件?
(2)商场第二次以原进价购进甲、乙两种商品,购进乙种商品的件数不变,而购进甲种商品的件数是第一次的2倍,甲种商品按原售价出售,而乙种商品打折销售.若两种商品销售完毕,要使第二次经营活动获利不少于8160元,乙种商品最低售价为每件多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com