
����Ŀ��Ϊ�����ҹ�����ά�Ͳ��ӹٱ����������ͨ��A�ۿڡ�B�ۿڷֱ�����100�ֺ�50���������ʣ���֪�������ڼײֿ����80�֣��Ҳֿ����70�֣����Ӽס������ֿ��������ʵ��ۿ�A�ķ��÷ֱ�Ϊ14Ԫ/�֣�20Ԫ/�֣��Ӽס������ֿ��������ʵ��ۿ�B�ķ��÷ֱ�Ϊ10Ԫ/�֡�8Ԫ/�֣�
������Ӽײֿ�����A�ۿ�x�֣�����д����
��һ
�ۿ� | �Ӽײֿ��ˣ��֣� | ���Ҳֿ��ˣ��֣� |
A�� | �� �� | �� �� |
B�� | �� �� | �� �� |
����
�ۿ� | �Ӽײֿ��˵��ۿڷ��ã�Ԫ�� | ���Ҳֿ��˵��ۿڷ��ã�Ԫ�� |
A�� | 14x | �� �� |
B�� | �� �� | �� �� |
����������ɴ˴�������������ʡ���õĵ��䷽������˵�����ɣ�
���𰸡�����x��100��x��80��x��x��30��20��100��x����10��80��x����8��x��30�������Ѽײֿ��ȫ������A�ۿڣ��ٴ��Ҳֿ���20����A�ۿڣ��Ҳֿ�����µ�ȫ������B�ۿڣ����ɼ�����
��������
���������������ʾ���ײֿ���Ҳֿ�ֱ�����A��B���ۿڵ������������ɵ�����ϵ�����˷�=�ײֿ�����A�ۿڵķ���+�ײֿ�����B�ۿڵķ���+�Ҳֿ�����A�ۿڵķ���+�Ҳֿ�����B�ۿڵķ�����ʽ�����������ݲ���ʽ��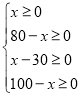 �ó�x��ȡֵ��
�ó�x��ȡֵ��
��������Ϊ���õĺ���Ϊһ�κ������������Կ�֪��y��x��������٣���x=80ʱ��y��С���������Сֵ��д�����䷽����
������Ӽײֿ���x����A�ۿڣ���Ӽײֿ�����B�ۿڵ��У�80��x���֣����Ҳֿ�����A�ۿڵ��У�100��x���֣�����B�ۿڵ���50����80��x��=��x��30���֣�
���÷ֱ�Ϊ14xԪ��10��80��x��Ԫ��20��100��x��Ԫ��8��x��30��Ԫ��
�ʴ𰸷ֱ�Ϊx��100��x��80��x��x��30��20��100��x����10��80��x����8��x��30����
������Ϊy=14x+20��100��x��+10��80��x��+8��x��30��=��8x+2560��
�������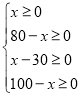 ��
��
��x��ȡֵ��Χ��30��x��80��
��Ϊy��x��������٣����Ե�x=80ʱ���˷���С��
��x=80ʱ��y=��8��80+2560=1920��
��ʱ����Ϊ���Ѽײֿ��ȫ������A�ۿڣ��ٴ��Ҳֿ���20����A�ۿڣ��Ҳֿ�����µ�ȫ������B�ۿڣ�


 �ǻ�С��ϰϵ�д�
�ǻ�С��ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
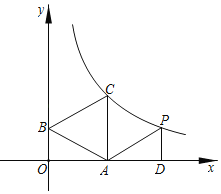
����Ŀ����ͼ��һ�κ���y����![]() x+2��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱ���ABC��
x+2��ͼ����x�ᡢy��ֱ��ڵ�A��B�����߶�ABΪ���ڵ�һ�������ȱ���ABC��
��1������C�ڷ���������y��![]() ��ͼ���ϣ���÷����������Ľ���ʽ��
��ͼ���ϣ���÷����������Ľ���ʽ��
��2����P��4![]() ��m���ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD����OAB������P���ڣ�1���з���������ͼ����ʱ�����P�����꣮
��m���ڵ�һ���ޣ�����P��x��Ĵ��ߣ�����ΪD������PAD����OAB������P���ڣ�1���з���������ͼ����ʱ�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
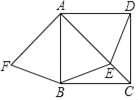
����Ŀ����ͼ��������ABCD������E��AC�ϣ�AF��AC������ΪA��AF��AE��
��1��BF��DE��������������ϵ����֤����Ľ��ۣ�
��2�����������������ֲ����������£�����E�˶���AC�е�ʱ���ı���AFBE��ʲô�����ı��Σ���֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
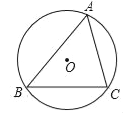
����Ŀ����ͼ����ABC�ڽ�����O��
��1������B��ƽ��������O���ڵ�D���ó߹���ͼ������д��������Ҫ������ͼ�ۼ�����
��2���ڣ�1����������AD������BAC=60������C=66��������DAC�Ĵ�С��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�Ƶ�B��ʱ����ת30����õ�������BEFG��EF��AD�ཻ�ڵ�H���ӳ�DA��GF�ڵ�K����������ABCD�߳�Ϊ![]() ����HD�ij�Ϊ____����
����HD�ij�Ϊ____����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
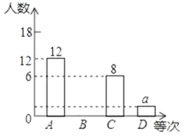
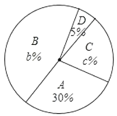
����Ŀ��2020�꣬һ��ͻȻ����������״�������������赲��ѧ���ǿ�ѧ�ĽŲ������ѧУ�����ˡ�ս���ڼң����Ͽ��á������֤ѧ����У����ѧ��Ϊ���ٳ�����������թƭ�İ��������Ҫ��ѧ�����շ�թƭ֪ʶ���������������Ϊ�˽�ijУѧ���IJ�����������������ȡ����ѧ���ijɼ�����ͳ�ƣ����Ѳ��Գɼ���ΪA��B��C��D�ĸ��ȴΣ����Ƴ���ͼ��ʾ�IJ�������ͳ��ͼ��������ͼ����������⣺
��1��a= ��b= ��c= ��
��2���뽫����ͳ��ͼ�����������������ʾC�ȴε��������Ե�Բ�ĽǵĶ�����
��3��ѧУ������A�ȴεļס��ҡ�����������ѧ���У����ѡȡ����ѧ���μ�ȫ����ѧ��������թƭ֪ʶ�����������б�������״ͼ������ס�������ѧ��ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳��ס��ҡ�������ҵ��Ա5���µ����۶��λ����Ԫ�����±���

��ס��ҡ�������ҵ��Ա�����۶����ȶ�����___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ⱳ������![]() �У�
�У�![]() ���ϵĶ���
���ϵĶ���![]() ��
��![]() ��
��![]() �˶�����
�˶�����![]() ��
��![]() ���غϣ�����
���غϣ�����![]() ���
���![]() ͬʱ�������ɵ�
ͬʱ�������ɵ�![]() ��
��![]() ���ӳ��߷����˶���
���ӳ��߷����˶���![]() ����
����![]() �غϣ�������
�غϣ�������![]() ��
��![]() �ڵ�
�ڵ�![]() ����
����![]() ���߶�
���߶�![]() ��һ��.
��һ��.
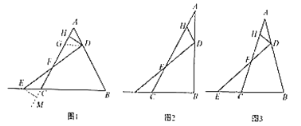
��1���������ԣ���ͼ����![]() �ǵȱ������Σ�
�ǵȱ������Σ�![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ���ȣ���֤��
���˶��ٶ���ȣ���֤��![]() .
.
С��ͬѧ���ֿ�������������˼·��������⣺
˼·һ������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ����֤
����֤![]() ����֤
����֤![]() ���Ӷ�֤�ý��۳�����
���Ӷ�֤�ý��۳�����
˼·��������![]() ��
��![]() ����
����![]() ���ӳ����ڵ�
���ӳ����ڵ�![]() ����֤
����֤![]() ����֤
����֤![]() ���Ӷ�֤�ý��۳���.
���Ӷ�֤�ý��۳���.
������ѡһ��˼·����������д��С���֤�����̣��������ַ����������Ե�һ�ַ������֣�
��2�����̽������ͼ������![]() �У�
��![]() ��
��![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ�֮����
���˶��ٶ�֮����![]() ����
����![]() ��ֵ��
��ֵ��
��3��������չ����ͼ������![]() �У�
��![]() ��
��![]() ����
����![]() ���ҵ�
���ҵ�![]() ��
��![]() ���˶��ٶ���ȣ����ú�
���˶��ٶ���ȣ����ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ��ֱ��д�����������д�����̣�.
��ֱ��д�����������д�����̣�.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com