
【题目】如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为![]() ,则HD的长为____ .
,则HD的长为____ .

【答案】![]() ﹣1
﹣1
【解析】
连接BH,由正方形的性质得出∠BAH=∠ABC=∠BEH=∠F=90°,由旋转的性质得:AB=EB,∠CBE=30°,得出∠ABE=60°,由HL证明Rt△ABH≌Rt△EBH,得出∠ABH=∠EBH=![]() ∠ABE=30°,AH=EH,由三角函数求出AH,即可得出HD的长.
∠ABE=30°,AH=EH,由三角函数求出AH,即可得出HD的长.
连接BH,如图所示:
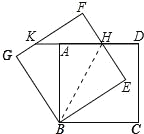
∵四边形ABCD和四边形BEFG是正方形,
∴∠BAH=∠ABC=∠BEH=∠F=90°,
由旋转的性质得:AB=EB,∠CBE=30°,
∴∠ABE=60°,
在Rt△ABH和Rt△EBH中,![]() ,
,
∴Rt△ABH≌△Rt△EBH(HL),
∴∠ABH=∠EBH=![]() ∠ABE=30°,AH=EH,
∠ABE=30°,AH=EH,
∴AH=ABtan∠ABH=![]() ×
×![]() =1,
=1,
∴HD=AD﹣AH=![]() ﹣1,
﹣1,
故答案为:![]() ﹣1.
﹣1.


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=60°,AB=6,点M为AB边上一点,AM=4,点N为AD边上的一动点,沿MN将△AMN翻折,点A落在点P处,当点P在菱形的对角线上时,AN的长度为_____.
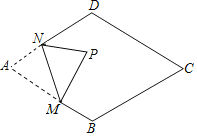
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一条抛物线与x轴相交于M,N两点(点M在点N的左侧),其顶点P在线段AB上移动,点A,B的坐标分别为(-2,-3),(1,-3),点N的横坐标的最大值为4,则点M的横坐标的最小值为( )

A.-1 B.-3C.-5D.-7
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“勤劳”是中华民族的传统美德,学校要求同学们在家里帮助父母做一些力所能及的家务.在本学期开学初,小颖同学随机调查了部分同学寒假在家做家务的总时间,设被调查的每位同学寒假在家做家务的总时间为x小时,将做家务的总时间分为五个类别:A(0≤x<10),B(10≤x<20),C(20≤x<30),D(30≤x<40),E(x≥40).并将调查结果制成如下两幅不完整的统计图:
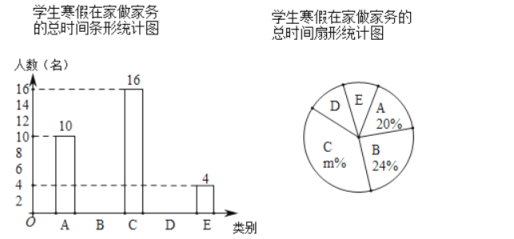
根据统计图提供的信息,解答下列问题:
(1)本次共调查了 名学生;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)扇形统计图中m的值是 ,类别D所对应的扇形圆心角的度数是 度;
(4)若该校有800名学生,根据抽样调查的结果,请你估计该校有多少名学生寒假在家做家务的总时间不低于20小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在国家的宏观调控下,某市的商品房成交价由今年3月份的5000元/m2下降到5月份的4050元/m2.
(1)问4、5两月平均每月降价的百分率是多少?
(2)如果房价继续回落,按此降价的百分率,你预测到7月分该市的商品房成交均价是否会跌破3000元/m2?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为保障我国海外维和部队官兵的生活,现需通过A港口、B港口分别运送100吨和50吨生活物资.已知该物资在甲仓库存有80吨,乙仓库存有70吨,若从甲、乙两仓库运送物资到港口A的费用分别为14元/吨,20元/吨;从甲、乙两仓库运送物资到港口B的费用分别为10元/吨、8元/吨.
(Ⅰ)设从甲仓库运往A港口x吨,试填写表格.
表一
港口 | 从甲仓库运(吨) | 从乙仓库运(吨) |
A港 |
|
|
B港 |
|
|
表二
港口 | 从甲仓库运到港口费用(元) | 从乙仓库运到港口费用(元) |
A港 | 14x |
|
B港 |
|
|
(Ⅱ)给出能完成此次运输任务的最节省费用的调配方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,AB是⊙O的直径,点C为⊙O上一点,![]() 于点F,交⊙O于点E,AC交BE于点H,点D为OE延长线上的一点,且∠ODA=∠BEC.
于点F,交⊙O于点E,AC交BE于点H,点D为OE延长线上的一点,且∠ODA=∠BEC.
(1)求证:AD是⊙O的切线;
(2)求证:![]() ;
;
(3)若⊙O的半径为5,![]() ,求AH的长.
,求AH的长.
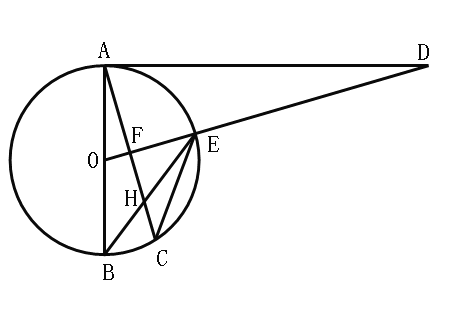
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B在反比例函数y=![]() (x>0)的图象上,点C,D在反比例函数y=
(x>0)的图象上,点C,D在反比例函数y=![]() (k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为
(k>0)的图象上,AC∥BD∥y轴,已知点A,B的横坐标分别为1,2,△OAC与△ABD的面积之和为![]() ,则k的值为_____.
,则k的值为_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com