
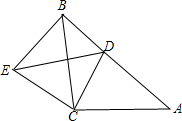
 如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.
如图,△ABC与△CDE均是等腰直角三角形,∠ACB=∠DCE=90°,D在AB上,连接BE.分析 (1)由△ABC与△CDE均是等腰直角三角形可得AC=BC、CD=CE,根据∠ACB=∠DCE=90°得∠ACD=∠BCE,根据SAS可判定△ACD≌△BCE;
(2)由(1)知S△ACD=S△BCE,而S四边形BDCE=S△BCE+S△BCD,可知S四边形BDCE=S△ACD+S△BCD=S△ABC.
解答 解:(1)∵∠ACB=∠DCE=90°,即∠ACD+∠BCD=∠BCE+∠BCD,
∴∠ACD=∠BCE,
又∵△ABC与△CDE均是等腰直角三角形,
∴AC=BC,CD=CE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE(SAS);
(2)∵△ABC是等腰直角三角形,且AB=$\sqrt{2}$,
∴AC=BC=1,
∵△ACD≌△BCE,
∴S△ACD=S△BCE,
∵S四边形BDCE=S△BCE+S△BCD,
∴S四边形BDCE=S△ACD+S△BCD=S△ABC=$\frac{1}{2}$×1×1=$\frac{1}{2}$.
点评 本题主要考查等腰三角形的性质及全等三角形的判定和性质的应用,熟练掌握全等三角形的5种判定方法:SSS、SAS、AAS、ASA、HL是关键,选用何种方法,取决于题目中的已知条件.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
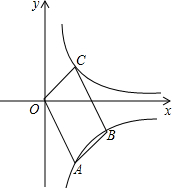 如图所示,四边形OABC为平行四边形,点A、B在反比例函数y=$\frac{{k}_{1}}{x}$图象上,点A(2,-4),边BC与x轴交于点D且D为BC中点,点C在反比例函数y=$\frac{{k}_{2}}{x}$图象上,则k2的值为( )
如图所示,四边形OABC为平行四边形,点A、B在反比例函数y=$\frac{{k}_{1}}{x}$图象上,点A(2,-4),边BC与x轴交于点D且D为BC中点,点C在反比例函数y=$\frac{{k}_{2}}{x}$图象上,则k2的值为( )| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
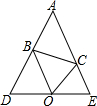 已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:
已知:△ABC中,∠ABC与∠ACB外角平分线交于点O,过O作直线交AB,AC延长线于点D,E,且AD=AE.求证:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
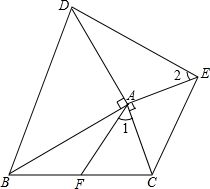 将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证:
将两块等腰直角三角板△ABD,△ACE如图摆放,0°<∠BAC<180°,连接BC,DE,AF是△ABC的中线.求证:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
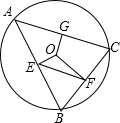 如图,⊙O的半径是7,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线段,垂足为E、F、G,连接EF.若OG=4,则EF为$\sqrt{33}$.
如图,⊙O的半径是7,△ABC是⊙O的内接三角形,过圆心O分别作AB、BC、AC的垂线段,垂足为E、F、G,连接EF.若OG=4,则EF为$\sqrt{33}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 调查某班学生对“五个重庆”的知晓率 | |
| B. | 调查一架“纤20”隐形战机各零部件的质量 | |
| C. | 调查2016年里约热内卢奥运会100米决赛参赛运动员兴奋剂的使用情况 | |
| D. | 调查涪陵市民对涪陵电视台《晚间播报》栏目的收视率 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com