
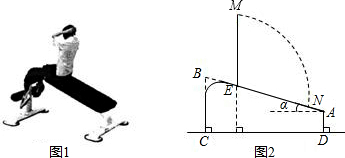
分析 (1)过A作AF∥DC,分别交BC,NE延长线于F,H,则四边形AFCD为矩形,AF=CD,AD=CF,可求得BF,在直角三角形ABF中,已知两边,满足解直角三角形的条件,就可求得α的值;
(2)由在直角三角形中两个锐角互余,求得∠NEM的度数,由弧长公式求得弧MN的长.
解答 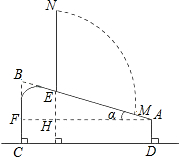 解:(1)过A作AF∥DC,分别交BC,NE延长线于F,H
解:(1)过A作AF∥DC,分别交BC,NE延长线于F,H
∵AD⊥CD,BC⊥CD
∴AD∥BC
∴四边形AFCD为矩形
∴BF=BC-AD=0.4.
在Rt△ABF中,
∵sinα=$\frac{BF}{AB}$=$\frac{0.4}{1.29}$≈0.310,
∴α≈18°.
即AB的倾斜角度数约为18°;
(2)∵NE⊥AF,
∴∠AEH=90°-18°=72°.
∴∠MEN=180°-∠AEH=108°.
∴$\widehat{MN}$的长=$\frac{108π×0.88}{180}$≈1.66(米).
答:小明头顶运动的路径$\widehat{MN}$的长约为1.60米.
点评 此题主要考查了解直角三角形的应用,熟练应用锐角三角函数的概念和弧长公式是解题关键.


科目:初中数学 来源: 题型:选择题
| A. | 1.58×105 | B. | 1.58×l04 | C. | 158×103 | D. | 0.158×106 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com