
【题目】如图,点Р是边长为2的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,![]() 的最小值是( )
的最小值是( )
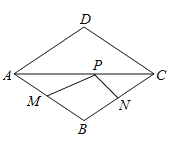
A.1B.![]() C.2D.
C.2D.![]()
科目:初中数学 来源: 题型:
【题目】读句画图并完成计算:如图,直线AB与直线CD交于点C ,

(1)过点P作PQ∥CD,交AB于点Q;
(2)过P作PR⊥CD于点R;
(3)若∠DCB=150,求∠PQC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年的6月5日为世界环保日,为了提倡低碳环保,某公司决定购买10台节省能源的新设备,现有甲、乙两种型号的设备可供选购. 经调查:购买3台甲型设备比购买2台乙型设备多花16万元,购买2台甲型设备比购买3台乙型设备少花6万元.
(1)求甲、乙两种型号设备的价格;
(2)该公司经预算决定购买节省能源的新设备的资金不超过110万元,你认为该公司有哪几种购买方案;
(3)在(2)的条件下,已知甲型设备的产量为240吨/月,乙型设备的产量为180吨/月.若每月要求总产量不低于2040吨,为了节约资金,请你为该公司设计一种最省钱的购买方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠BAD=∠CAE=90o,AB=AD,AE=AC, AF⊥CF,垂足为F.
(1)若AC=10,求四边形ABCD的面积;
(2)求证:AC平分∠ECF;
(3)求证:CE=2AF .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.
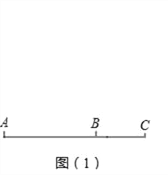
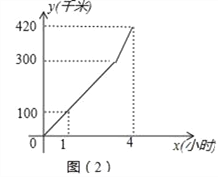
(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光集团新进了20台电视机和30台电饭煲,计划将这50台电器调配给下属的甲、乙两个商店销售,其中40台给甲商店,10台给乙商店.两个商店销售这两种电器每台的利润(元)如下表:
电视机 | 电饭煲 | |
甲商店/元 | 100 | 60 |
乙商店/元 | 80 | 50 |
(1)设集团调配给甲商店x台电视机,则调配给甲商店电饭煲 台,调配给乙商店电视机 台、电饭煲 台;
(2)求出x的取值范围;
(3)如果阳光集团卖出这50台电器想要获得的总利润为3650元,请求出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个由正奇数排成的数阵.用如图所示的四边形框去框住四个数.

(1)若设框住四个数中左上角的数为n,则这四个数的和为 (用n的代数式表示);
(2)平行移动四边形框,若框住四个数的和为228,求出这4个数;
(3)平行移动四边形框,能否使框住四个数的和为508?若能,求出这4个数;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,直线y=12x+2与![]() 交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
交坐标轴于A,B两点.以AB为斜边在第一象限作等腰直角三角形ABC,C为直角顶点,连接OC.
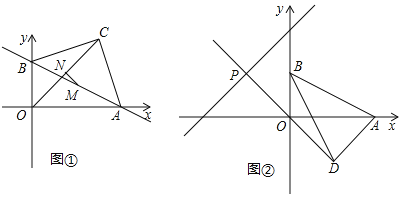
(1)求线段AB的长度
(2)求直线BC的解析式;
(3)如图②,将线段AB绕B点沿顺时针方向旋转至BD,且![]() ,直线DO交直线y=x+3
,直线DO交直线y=x+3![]() 于P点,求P点坐标.
于P点,求P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DCB中,∠A=∠D=90°,AC=BD,AC与BD相交于点O,限用无刻度直尺完成以下作图:
(1)在图1中作线段BC的中点P;
(2)在图2中,在OB、OC上分别取点E、F,使EF∥BC.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com