
分析 (1)利用平均数的定义求出即可;
(2)根据题意,分别计算甲乙两个人的方差可得,甲的方差小于乙的方差;
(3)结合平均数以及方差的意义,进而分析两人的成绩即可.
解答 解:(1)$\overline{{x}_{甲}}$=$\frac{1}{10}$(8+6+7+8+9+10+6+5+4+7)=7(分),
$\overline{{x}_{乙}}$=$\frac{1}{10}$(7+9+8+5+6+7+7+6+7+8)=7(分);
(2)${s}_{甲}^{2}$=$\frac{1}{10}$[(8-7)2+(6-7)2+…+(7-7)2]=3,
${s}_{乙}^{2}$=$\frac{1}{10}$[(7-7)2+(9-7)2+…+(8-7)2]=1.2;
(3)从平均成绩看,$\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$=$\frac{1}{10}$,甲乙成绩一样好,
从方差来看,${s}_{甲}^{2}$>${s}_{乙}^{2}$,乙的成绩更稳定.
点评 本题考查了平均数定义以及方差的定义与意义:一般地设n个数据,x1,x2,…xn的平均数为$\overline{x}$,则方差S2=$\frac{1}{n}$[(x1-$\overline{x}$)2+(x2-$\overline{x}$)2+…+(xn-$\overline{x}$)2],它反映了一组数据的波动大小,方差越大,波动性越大,反之也成立.


科目:初中数学 来源: 题型:选择题
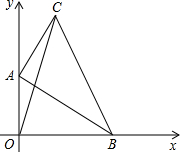 如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )
如图,在平面直角坐标系中,Rt△ABC的直角顶点A和顶点B分别在y轴正半轴及x轴正半轴上运动,若AB=4,AC=3,则在运动过程中,线段OC的最大值是( )| A. | 5 | B. | 2+$\sqrt{13}$ | C. | $\sqrt{13}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{(-5)^{2}}$=-5 | B. | $\sqrt{9}$=±3 | C. | $\root{3}{(-2)^{3}}$=-2 | D. | (2$\sqrt{3}$)2=6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com