
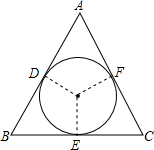
 如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.
如图,在△ABC中,AB=AC,⊙O是△ABC的内切圆,它与AB,BC,CA分别相切于点D、E、F.若∠ACB=90°,AB=AC=2,求圆的半径.| 2 |
| 2 |
| 2 |
 连结OD、OE、OF,设⊙O的半径为r,
连结OD、OE、OF,设⊙O的半径为r,| 2 |
| 2 |
| 2 |
| 2 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| 桌子张数 | 3 | 4 | 5 | n |
| 可坐人数 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 观察时间x | 该地区沙漠面积y(万公顷) |
| 第一年底 | 100.2 |
| 第二年底 | 100.4 |
| 第三年底 | 100.6 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:
甲乙两车分别从A、B两地同时出发相向而行.乙车出发1小时后出现故障,停下来维修半小时后继续前行.甲乙两车距A地的路程y1(千米)、y2(千米)与出发时间x(时)之间的函数图象如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,在直角坐标系中,每个小正方形的边长都是单位1.
如图,在直角坐标系中,每个小正方形的边长都是单位1.查看答案和解析>>
科目:初中数学 来源: 题型:
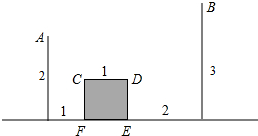 如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于
如图,某人A点出发去河里取水,然后再送到B点处,阴影部分CDEF是一座不能通行的正方形建筑,其余数据如图所示,那么他从A到B要走过的最短长度等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com