
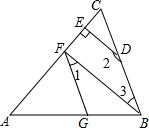
 已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E.
已知:如图,∠AGF=∠ABC,∠1+∠2=180°,DE⊥AC于点E. 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
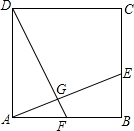 如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.
如图,已知点E、F分别为正方形ABCD的边BC、AB上的点,且AF=BE,AE与DF交于点G,试猜想AE与DF之间的大小关系和位置关系,并证明你的猜想.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
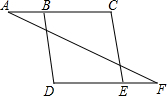 如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.
如图,已知∠A=∠F,∠C=∠D,试说明BD∥CE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
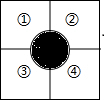 如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.
如图,一方形花坛分成编号为①、②、③、④四块,现有红、黄、蓝、紫四种颜色的花供选种.要求每块只种一种颜色的花,且相邻的两块种不同颜色的花,如果编号为①的已经种上红色花,那么其余三块不同的种法有( )种.| A. | 10 | B. | 20 | C. | 21 | D. | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com