
【题目】如图,两个形状,大小完全相同的含有30°,60°的三角板如图①放置,PA,PB与直线MN重合,且三角板PAC与三角板PBD均可绕点P逆时针旋转。
(1)试说明:∠DPC=90°;
(2)如图②,若三角板PAC的边PA从PN处开始绕点P逆时针旋转一定度数,PF平分![]() ,PE平分
,PE平分![]() ,求
,求![]() 。
。
(3)如图③,若三角板PAC的边PA从PN处开始绕点P逆时针旋转,转速为3。/s。同时三角板PBD的边PB从PM处开始绕点P逆时针旋转,转速为2。/s,在两个三角板旋转过程中(PC转到与PM重合时,三角板都停止转运),问![]() 的值是否变化?若不变,求出其值,若变化,说明理由。
的值是否变化?若不变,求出其值,若变化,说明理由。

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10…)和“正方形数”(如1,4,9,16…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
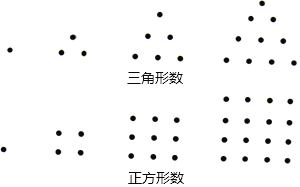
A. 33 B. 301 C. 386 D. 571
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:

(1)九(1)班的学生人数为40,并把条形统计图补充完整;
(2)扇形统计图中m=10,n=20,表示“足球”的扇形的圆心角是72度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度i(即tan∠ABC)为1:![]() ,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.
,点P、H、B、C、A在同一个平面上.点H、B、C在同一条直线上,且PH⊥HC.

(1)山坡坡角(即∠ABC)的度数等于 度;
(2)求山坡A、B两点间的距离(结果精确到0.1米).
(参考数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=![]() AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )
AB,∠BAD的平分线交BC于点E,DH⊥AE于点H,连接BH并延长交CD于点F,连接DE交BF于点O,下列结论:①∠AED=∠CED;②OE=OD;③BH=HF;④BC﹣CF=2HE;⑤AB=HF,其中正确的有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)求证:四边形ADEF是平行四边形;
(2)求证:∠DHF=∠DEF.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知菱形ABCD中,∠BAD=60°,点E、F分别是AB、AD上两个动点,若AE=DF,连接BF与DE相交于点G,连接CG,与BD相交于H。
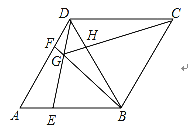
(1)求∠BGE的大小;(2)求证:GC平分∠BGD.
查看答案和解析>>
科目:初中数学 来源: 题型:
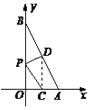
【题目】一次函数y=kx+b的图象与x、y轴分别交于点A(2,0),B(0,4).
(1)求该函数的解析式;
(2)O为坐标原点,设OA、AB的中点分别为C、D,P为OB上一动点,求PC+PD的最小值,并求取得最小值时P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
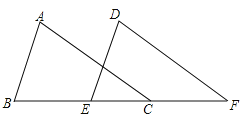
【题目】如图,在△ABC和△DEF中,AB=DE,AC=DF,BE=CF,且![]() ,
,![]() ,
,![]() ,
,![]() ,则下列结论中错误的有( )个
,则下列结论中错误的有( )个
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com