
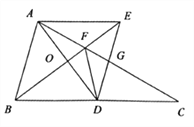
【题目】如图,在![]() 中,
中,![]() 是
是![]() 边上的中线,
边上的中线,![]() 是
是![]() 中点,过点
中点,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
(1)判断四边形![]() 的形状,并说明理由;
的形状,并说明理由;
(2)若![]() ,且
,且![]() ,求四边形
,求四边形![]() 的面积.
的面积.
(3)连接![]() ,求证:
,求证:![]() .
.
【答案】(1)四边形ABDE是菱形.理由见解析;(2)12;(3)见解析.
【解析】(1)先判定△AOE≌△DOB(ASA),得出AE=BD,根据AE∥BD,即可得出四边形ABDE是平行四边形,再根据BD=BA,即可得到平行四边形ABDE是菱形;
(2)根据四边形ABDE是菱形,AB=![]() ,且OA:OB=2:3,运用勾股定理求得AD=4,BE=6,即可得出菱形ABDE的面积;
,且OA:OB=2:3,运用勾股定理求得AD=4,BE=6,即可得出菱形ABDE的面积;
(3)根据菱形的性质得出∠GDF=∠DCF,再根据∠GFD=∠DFC,即可判定△DFG∽△CFD,进而得到![]() ,据此可得DF2=FGFC.
,据此可得DF2=FGFC.
(1)四边形ABDE是菱形.理由如下:
∵AE∥BC,∴∠EAO=∠BDO,∵O是AD中点,∴AO=DO,
在△AOE和△DOB中,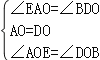 ,
,
∴△AOE≌△DOB(ASA),∴AE=BD,
又∵AE∥BD,∴四边形ABDE是平行四边形,
∵AD是BC边上的中线,∴BC=2BD,
又∵BC=2AB,∴BD=BA,∴平行四边形ABDE是菱形;
(2)∵四边形ABDE是菱形,∴AD⊥BE,AO=![]() AD,BO=
AD,BO=![]() BE,
BE,
设OA=2k,OB=3k,在Rt△AOB中,由勾股定理得,4k2+9k2=13,解得k=1,
∴OA=2,OB=3,∴AD=4,BE=6,
∴菱形ABDE的面积=![]() ×4×6=12;
×4×6=12;
(3)证明:∵四边形ABDE是菱形,
∴BE垂直平分AD,∴EA=ED,FA=FD,
∴∠EAO=∠EDO,∠FAO=∠FDO,∴∠EAF=∠EDF,
∵AE∥BC,∴∠EAO=∠DCF,∴∠GDF=∠DCF,
又∵∠GFD=∠DFC,
∴△DFG∽△CFD,
∴![]() =
=![]() ,∴DF2=FGFC.
,∴DF2=FGFC.


科目:初中数学 来源: 题型:
【题目】填空并在括号内加注理由。
如图,已知![]() ∥
∥![]() ,
,![]() 、
、![]() 分别平分
分别平分![]() 和
和![]()

求证:![]()
证明:∵![]() ∥
∥![]()
∴![]() = ( )
= ( )
∵![]() 、
、![]() 平分
平分![]() 、
、![]()
∴![]() =
=![]()
∴![]() =
=![]() ( )
( )
∴![]() =
=![]()
∴ ∥ ( )
∴![]() =∠ ( )
=∠ ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC和△MNB中,∠ACB=∠MBN=90°,AC=BC=4,MB=NB= ![]() BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG.
BC,点N在BC边上,连接AN,CM,点E,F,D,G分别为AC,AN,MN,CM的中点,连接EF,FD,DG,EG. 
(1)判断四边形EFDG的形状,并证明;
(2)如图2,将图1中的△MBN绕点B逆时针旋转90°,其他条件不变,猜想此时四边形EFDG的形状,并证明. 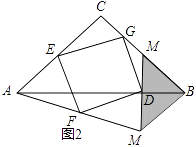
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需 ![]() 天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需
天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需 ![]() 天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围); 表一
粗加工数量/吨 | 3 | 7 | x |
精加工数量/吨 | 47 |
表二
粗加工数量/吨 | 3 | 7 | x |
粗加工获利/元 | 2800 | ||
精加工获利/元 | 25800 |
y与x的函数关系式
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发,沿
出发,沿![]() 向点
向点![]() 匀速运动,速度为每秒1个单位,过点
匀速运动,速度为每秒1个单位,过点![]() 作
作![]() ,交对角线
,交对角线![]() 于点
于点![]() .点
.点![]() 从点
从点![]() 出发,沿对角线
出发,沿对角线![]() 向点
向点![]() 匀速运动,速度为每秒1个单位.
匀速运动,速度为每秒1个单位. ![]() 、
、![]() 两点同时出发,设它们的运动时间为
两点同时出发,设它们的运动时间为![]() 秒(
秒(![]() ).
).
(1)当![]() 时,求出
时,求出![]() 的值;
的值;
(2)连接![]() ,当
,当![]() 时,求出
时,求出![]() 的值;
的值;
(3)试探究:当![]() 为何值时,
为何值时,![]() 是等腰三角形?
是等腰三角形?


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂一周计划每日生产某产品100吨,由于工人实行轮休,每日上班人数不一定相等,实际每日生产量与计划量相比情况如下表(以计划量为标准,增加的吨数记为正数,减少的吨数记为负数)
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减/吨 | ﹣1 | +3 | ﹣2 | +4 | +7 | ﹣5 | ﹣10 |
(1)生产量最多的一天比生产量最少的一天多生产多少吨?
(2)本周总生产量是多少吨?比原计划增加了还是减少了?增减数为多少吨?
(3)若本周总生产的产品全部由35辆货车一次性装载运输离开工厂,则平均每辆货车大约需装载多少吨?(结果精确到0.01吨)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字1,2,3,4,如图2,正方形ABCD顶点处各有一个圈,跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长. 例如:若从圈A起跳,第一次掷得3,就顺时针连续跳3个边长,落到圈D,若第二次掷得2,就从D开始顺时针连续跳2个边长,落到圈B,…设游戏者从圈A起跳.
(1)若随机掷一次骰子,求落回到圈A的概率P1;
(2)若随机掷两次骰子,用列表法或树状图法求出最后落回到圈A的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点M、N是∠ABC与∠ACB三等分线的交点.若∠A=60°,则∠BMN的度数为( )

A. 45° B. 50° C. 60° D. 65°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com