
【题目】如图,已知∠1+∠2﹦180°,∠3﹦∠B,则DE∥BC,下面是王华同学的推导过程﹐请你帮他在括号内填上推导依据或内容.

证明:
∵∠1+∠2﹦180(已知),
∠1﹦∠4 (_________________),
∴∠2﹢_____﹦180°.
∴EH∥AB(___________________________________).
∴∠B﹦∠EHC(________________________________).
∵∠3﹦∠B(已知)
∴ ∠3﹦∠EHC(____________________).
∴ DE∥BC(__________________________________).
【答案】对顶角相等;同旁内角互补,两直线平行;两直线平行,同位角相等;等量代换;内错角相等,两直线平行
【解析】试题分析:根据对顶角相等,得出∠1=∠4,根据等量代换可知∠2+∠4=180°,根据同旁内角互补,两直线平行,得出EH∥AB,再由两直线平行,同位角相等,得出∠B=∠EHC,已知∠3=∠B,由等量代换可知∠3=∠EHC,再根据内错角相等,两直线平行,即可得出DE∥BC.
试题解析:∠1﹦∠4 ( 对顶角相等 ),
∴∠2﹢∠4﹦180°.
∴EH∥AB ( 同旁内角互补,两直线平行)
∴∠B﹦∠EHC(两直线平行,同位角相等 ).
∴ ∠3﹦∠EHC( 等量代换 ).
∴ DE∥BC(内错角相等,两直线平行).


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,1),B(-1,1),C(-1,-2),D(1,-2).把一条长为2016个单位长度且没有弹性的细线(线的粗细忽略不计)的一端固定在点A处,并按A-B-C-D…的规律绕在ABCD的边上,则细线另一端所在位置的点的坐标是( )

A. (0,-2) B. (-1,-1) C. (-1,0) D. (1,-2)
查看答案和解析>>
科目:初中数学 来源: 题型:
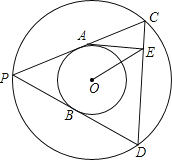
【题目】如图,以O为圆心的两个同心圆,大圆半径为5,小圆半径为![]() ,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
,点P为大圆上的一点,PC、PB切小圆于点A、点B,交大圆于C、D两点,点E为弦CD上任一点,则AE+OE的最小值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,O为直线AB上一点,OD平分∠AOC,∠DOE=90°.
(1)∠AOD的余角是 ______ ,∠COD的余角是 ______
(2)OE是∠BOC的平分线吗?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com