
【题目】图形变换中的数学,问题情境:在课堂上,兴趣学习小组对一道数学问题进行了深入探究,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AB的中点,连接CD.
(1)探索发现:
如图①,BC与BD的数量关系是;
(2)猜想验证:
如图②,若P是线段CB上一动点(点P不与点B,C重合),连接DP,将线段DP绕点D逆时针旋转60°,得到线段DF,连接BF,请猜想BF,BP,BD三者之间的数量关系,并证明你的结论;
(3)拓展延伸:
若点P是线段CB延长线上一动点,按照(2)中的作法,请在图③中补全图象,并直接写出BF、BP、BD三者之间的数量关系.
【答案】
(1)BC=BD
(2)
解:BF+BP=BD,
理由:∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC= ![]() AB,
AB,
∵点D是AB的中点,
∴BC=BD,
∴△DBC是等边三角形,
∴∠CDB=60°,DC=DB,
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
∴∠CDB﹣∠PDB=∠PDF﹣∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中, 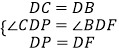 ,
,
∴△DCP≌△DBF,
∴CP=BF,
∵CP+BP=BC,
∴BF+BP=BC,
∵BC=BD,
∴BF+BP=BD
(3)
解:如图③,
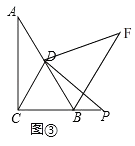
关系:BF=BD+BP,
理由:∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC= ![]() AB,
AB,
∵点D是AB的中点,
∴BC=BD,
∴△DBC是等边三角形,
∴∠CDB=60°,DC=DB,
∵线段DP绕点D逆时针旋转60°,得到线段DF,
∴∠PDF=60°,DP=DF,
∴∠CDB+∠PDB=∠PDF+∠PDB,
∴∠CDP=∠BDF,
在△DCP和△DBF中, 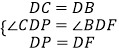 ,
,
∴△DCP≌△DBF,
∴CP=BF,
∵CP=BC+BP,
∴BF=BC+BP,
∵BC=BD,
∴BF=BD+BP.
【解析】解:(1)∵∠ACB=90°,∠A=30°,
∴∠CBA=60°,BC= ![]() AB,
AB,
∵点D是AB的中点,
∴BC=BD,
所以答案是:BC=BD;


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
【题目】如图,已知反比例函数y= ![]() (k1>0),y=
(k1>0),y= ![]() (k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为
(k2<0).点A在y轴的正半轴上,过点A作直线BC∥x轴,且分别与两个反比例函数的图象交于点B和C,连接OC、OB.若△BOC的面积为 ![]() ,AC:AB=2:3,则k1= , k2= .
,AC:AB=2:3,则k1= , k2= . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,点E,F分别是边BC,AB上的点,且CE=BF.连接DE,过点E作EG⊥DE,使EG=DE,连接FG,FC.
(1)请判断:FG与CE的数量关系是 , 位置关系是;
(2)如图2,若点E,F分别是边CB,BA延长线上的点,其它条件不变,(1)中结论是否仍然成立?请作出判断并给予证明;
(3)如图3,若点E,F分别是边BC,AB延长线上的点,其它条件不变,(1)中结论是否仍然成立?请直接写出你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3的对称轴是直线x=1.
(1)求证:2a+b=0;
(2)若关于x的方程ax2+bx﹣8=0的一个根为4,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.
(1)求足球和篮球的单价各是多少元?
(2)根据学校实际情况,需一次性购买足球和篮球共20个,但要求购买足球和篮球的总费用不超过1550元,学校最多可以购买多少个足球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1 , 它与x轴交于点O,A1;将C1绕点A1旋转180°得C2 , 交x轴于点A2;将C2绕点A2旋转180°得C3 , 交x轴于点A3;…,如此进行下去,直至得Cn . 若P(2014,m)在第n段抛物线Cn上,则m= 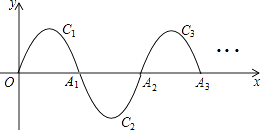
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知某道判断题的五个选项中有两个正确答案,该题满分为4分,得分规则是:选出两个正确答案且没有选错误答案得4分;只选出一个正确答案且没有选错误答案得2分;不选或所选答案中有错误答案得0分.
(1)任选一个答案,得到2分的概率是;
(2)请利用树状图或表格求任选两个答案,得到4分的概率;
(3)如果小明只能确认其中一个答案是正确的,此时的最佳答题策略是
A.只选确认的那一个正确答案
B.除了选择确认的那一个正确答案,再任选一个
C.干脆空着都不选了.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据卫生防疫部门要求,游泳池必须定期换水,清洗.某游泳池周五早上8:00打开排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11:30全部排完.游泳池内的水量Q(m2)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题: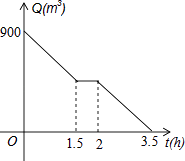
(1)暂停排水需要多少时间?排水孔排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com