
����Ŀ����ͼ1����������ABCD�У���E��F�ֱ��DZ�BC��AB�ϵĵ㣬��CE=BF������DE������E��EG��DE��ʹEG=DE������FG��FC��
��1�����жϣ�FG��CE��������ϵ�� �� λ�ù�ϵ����
��2����ͼ2������E��F�ֱ��DZ�CB��BA�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ�������������жϲ�����֤����
��3����ͼ3������E��F�ֱ��DZ�BC��AB�ӳ����ϵĵ㣬�����������䣬��1���н����Ƿ���Ȼ��������ֱ��д������жϣ�
���𰸡�
��1���⣺FG=CE��FG��CE
��2��
�⣺����G��GH��CB���ӳ����ڵ�H��

��EG��DE��
���GEH+��DEC=90�㣬
�ߡ�GEH+��HGE=90�㣬
���DEC=��HGE��
�ڡ�HGE���CED�У�
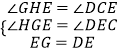 ��
��
���HGE�ա�CED��AAS����
��GH=CE��HE=CD��
��CE=BF��
��GH=BF��
��GH��BF��
���ı���GHBF�Ǿ��Σ�
��GF=BH��FG��CH
��FG��CE
���ı���ABCD�������Σ�
��CD=BC��
��HE=BC
��HE+EB=BC+EB
��BH=EC
��FG=EC
��3��
�⣺������
���ı���ABCD�������Σ�
��BC=CD����FBC=��ECD=90�㣬
�ڡ�CBF���DCE�У�
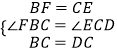 ��
��
���CBF�ա�DCE��SAS����
���BCF=��CDE��CF=DE��
��EG=DE��
��CF=EG��
��DE��EG
���DEC+��CEG=90��
�ߡ�CDE+��DEC=90��
���CDE=��CEG��
���BCF=��CEG��
��CF��EG��
���ı���CEGFƽ���ı��Σ�
��FG��CE��FG=CE��
����������1��ֻҪ֤���ı���CEGF��ƽ���ı��μ��ɵó�FG=CE��FG��CE����2�����츨���ߺ�֤����HGE�ա�CED�����ö�Ӧ�������֤�ı���GHBF�Ǿ��κ����õ��������������FG=C��FG��CE����3��֤����CBF�ա�DCE����֤���ı���CEGF��ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�������Ϊ2000Ԫ�ı�����2400Ԫ�۳���ƽ��ÿ�����۳�8̨��Ϊ����Ϲ��ҡ��ҵ����硱���ߵ�ʵʩ���̳�������ȡ�ʵ��Ľ��۴�ʩ��������������ֱ�����ۼ�ÿ����50Ԫ��ƽ��ÿ����ܶ��۳�4̨��
��1������ÿ̨���併��xԪ���̳�ÿ���������ֱ����������yԪ����д��y��x֮��ĺ�������ʽ������Ҫ��д�Ա�����ȡֵ��Χ��
��2���̳�Ҫ�������ֱ���������ÿ��ӯ��4800Ԫ��ͬʱ��Ҫʹ���յõ�ʵ�ݣ�ÿ̨����Ӧ���۶���Ԫ��
��3��ÿ̨���併�۶���Ԫʱ���̳�ÿ���������ֱ����������ߣ���������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA=3��OC=2����F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y= ![]() ��ͼ����BC�߽��ڵ�E��
��ͼ����BC�߽��ڵ�E�� 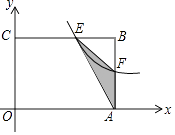
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���OABC�У�OA=3��OC=2����F��AB�ϵ�һ�����㣨F����A��B�غϣ�������F�ķ���������y= ![]() ��ͼ����BC�߽��ڵ�E��
��ͼ����BC�߽��ڵ�E�� 
��1����FΪAB���е�ʱ����ú����Ľ���ʽ��
��2����kΪ��ֵʱ����EFA���������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����������y= ![]() ��k��0����ͼ����3����1������1��y��3ʱ���Ա���x��ȡֵ��Χ�� ��
��k��0����ͼ����3����1������1��y��3ʱ���Ա���x��ȡֵ��Χ�� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ͼ�α任�е���ѧ�������龳���ڿ����ϣ���ȤѧϰС���һ����ѧ�������������̽������Rt��ABC�У���ACB=90�㣬��A=30�㣬��D��AB���е㣬����CD��
��1��̽�����֣�
��ͼ�٣�BC��BD��������ϵ����
��2��������֤��
��ͼ�ڣ���P���߶�CB��һ���㣨��P�����B��C�غϣ�������DP�����߶�DP�Ƶ�D��ʱ����ת60�㣬�õ��߶�DF������BF�������BF��BP��BD����֮���������ϵ����֤����Ľ��ۣ�
��3����չ���죺
����P���߶�CB�ӳ�����һ���㣬���գ�2���е�����������ͼ���в�ȫͼ��ֱ��д��BF��BP��BD����֮���������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ�������Ĵ���װ�к졢�ơ���������ɫ����100�������dz���ɫ�ⶼ��ͬ�����л���ĸ����ǰ��������2����5������֪�Ӵ�������һ������ĸ����� ![]() ��
��
��1������к���ĸ�����
��2����Ӵ�������һ�����ǰ���ĸ��ʣ�
��3��ȡ��5������5���������ʣ�����������һ�����Ǻ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ش���������⣺
�ⷽ�̣�x2��|x|��2=0��
�⣺��x��0ʱ��ԭ���̻�Ϊx2��x��2=0�����x1=2��x2=��1���������⣬��ȥ����
��x��0ʱ��ԭ���̻�Ϊx2+x��2=0�����x1=��2��x2=1���������⣬��ȥ����
��ԭ���̵ĸ���x1=2��x2=��2��
���������ⷽ��x2+|x��4|��8=0��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com