
【题目】已知:如图,以等边三角形ABC一边AB为直径的⊙O与边AC、BC分别交于点D、E,过点D作DF⊥BC,垂足为F. 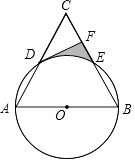
(1)求证:DF为⊙O的切线;
(2)若等边三角形ABC的边长为4,求DF的长;
(3)写出求图中阴影部分的面积的思路.(不求计算结果)
【答案】
(1)证明:连接OD,如图,
∵△ABC为等边三角形,
∴∠A=∠C=60°,
∵OA=OD,
∴∠ODA=∠A=60°,
∴∠ODA=∠C,
∴OD∥BC,
∵DF⊥BC,
∴OD⊥BC,
∴DF为⊙O的切线
(2)解:∵等边三角形ABC的边长为4,
∴AB=AC=4,∠C=60°,
∵AO=AD=2,
∴CD=2,
在Rt△CDF中,∵sinC= ![]() ,
,
∴DF=2sin60°= ![]()
(3)解:连接OE,如图,
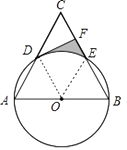
∵CF= ![]() CD=1,
CD=1,
∴EF=CE﹣CF=1,
∴S阴影部分=S梯形ODFE﹣S扇形DOE= ![]() (1+2)
(1+2) ![]() ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() π.
π.
【解析】(1)连接OD,如图,利用等边三角形的性质得到∠A=∠C=60°,再证明OD∥BC,然后利用DF⊥BC可得OD⊥BC,再根据切线的判定定理可判断DF为⊙O的切线;(2)利用等边三角形的性质得到AB=AC=4,∠C=60°,则CD=2,然后在Rt△CDF中利用正弦的定义可计算出DF;(3)连接OE,如图,根据扇形的面积公式,利用S阴影部分=S梯形ODFE﹣S扇形DOE进行计算.
【考点精析】掌握等边三角形的性质和切线的判定定理是解答本题的根本,需要知道等边三角形的三个角都相等并且每个角都是60°;切线的判定方法:经过半径外端并且垂直于这条半径的直线是圆的切线.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
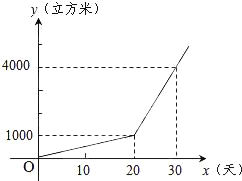
【题目】某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系式如图所示.
(1)第20天的总用水量为多少米3?
(2)当x≥20时,求y与x之间的函数关系式;
(3)种植时间为多少天时,总用水量达到7000米3?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】同学们,足球是世界上第一大运动,你热爱足球运动吗?已知在足球比赛中,胜一场得3分,平一场得1分,负一场得0分,一队共踢了30场比赛,负了9场,共得47分,那么这个队胜了( )
A. 10场 B. 11场 C. 12场 D. 13场
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠ACB为锐角.点D为射线BC上一动点,连接AD,将线段AD绕点A逆时针旋转90°得到AE,连结EC.如果AB=AC,∠BAC=90°. ①当点D在线段BC上时(与点B不重合),如图1,请你判断线段CE、BD之间的位置和数量关系(直接写出结论);
②当点D在线段BC的延长线上时,请你在图2画出图形,判断①中的结论是否仍然成立,并证明你的判断.
查看答案和解析>>
科目:初中数学 来源: 题型:
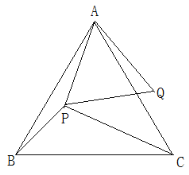
【题目】已知,点P是等边△ABC内一点,PA=4,PB=3,PC=5.线段AP绕点A逆时针旋转60°到AQ,连接PQ.(1)求PQ的长。(2)求∠APB的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上,A、B两点表示的数a,b满足|a﹣6|+(b+12)2=0
(1)a= ,b= ;
(2)若小球M从A点向负半轴运动、小球N从B点向正半轴运动,两球同时出发,小球M运动的速度为每秒2个单位,当M运动到OB的中点时,N点也同时运动到OA的中点,则小球N的速度是每秒 个单位;
(3)若小球M、N保持(2)中的速度,分别从A、B两点同时出发,经过 秒后两个小球相距两个单位长度.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列各式:
13+23=1+8=9,而(1+2)2=9,∴13+23=(1+2)2;
13+23+33=36,而(1+2+3)2=36,∴13+23+33=(1+2+3)2;
13+23+33+43=100,而(1+2+3+4)2=100,∴13+23+33+43=(1+2+3+4)2;
∴13+23+33+43+53=(______ )2= ______ .
根据以上规律填空:
(1)13+23+33+…+n3=(______ )2=[ ______ ]2.
(2)猜想:113+123+133+143+153= ______ .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com