
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD,将△BCD绕点B逆时针旋转60,得到△BAE,连接ED,若BC=5,BD=4,则有以下四个结论:①△BDE是等边三角形;②AE∥BC;③△ADE的周长是9;④∠ADE=∠BDC。其中正确结论的序号是( )

A. ②③④ B. ①③④ C. ①②④ D. ①②③
【答案】D
【解析】
先由△BCD绕点B逆时针旋转60°,得到△BAE得到BD=BE,∠DBE=60°,则可判断△BDE是等边三角形;根据等边三角形的性质得BA=BC,∠ABC=∠C=∠BAC=60°,再根据旋转的性质得到∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,所以∠BAE=∠ABC=60°,则根据平行线的判定方法即可得到AE∥BC;根据等边三角形的性质得∠BDE=60°,而∠BDC>60°,则可判断∠ADE≠∠BDC;由△BDE是等边三角形得到DE=BD=4,再利用△BCD绕点B逆时针旋转60°,得到△BAE,则AE=CD,所以△AED的周长=AE+AD+DE=CD+AD+DE=AC+BD.
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴BD=BE,∠DBE=60°,
∴△BDE是等边三角形,所以①正确;
∵△ABC为等边三角形,
∴BA=BC,∠ABC=∠C=∠BAC=60°,
∵△BCD绕点B逆时针旋转60°,得到△BAE,
∴∠BAE=∠BCD=60°,∠BCD=∠BAE=60°,
∴∠BAE=∠ABC,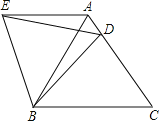
∴AE∥BC,所以②正确;
∴∠BDE=60°,
∵∠BDC=∠BAC+∠ABD>60°,
∴∠ADE≠∠BDC,所以④错误;
∵△BDE是等边三角形,
∴DE=BD=4,
而△BCD绕点B逆时针旋转60°,得到△BAE,
∴AE=CD,
∴△AED的周长=AE+AD+DE=CD+AD+DE=AC+4=5+4=9,所以③正确;
故选:D.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,ABCD中,AE平分∠BAD,交BC于E,DE⊥AE,下列结论::①DE平分∠ADC;②E是BC的中点;③AD=2CD;④梯形ADCE的面积与△ABE的面积比是3:1,其中正确的结论的个数有( )

A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在距离铁轨200米的B处,观察由南宁开往百色的“和谐号”动车,当动车车头在A处时,恰好位于B处的北偏东60°方向上;10秒钟后,动车车头到达C处,恰好位于B处的西北方向上,则这时段动车的平均速度是( )米/秒.
A.20( ![]() +1)
+1)
B.20( ![]() ﹣1)
﹣1)
C.200
D.300
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,轮船在A处观测灯塔C位于北偏西70°方向上,轮船从A处以每小时20海里的速度沿南偏西50°方向匀速航行,1小时后到达码头B处,此时,观测灯塔C位于北偏西25°方向上,则灯塔C与码头B的距离是( )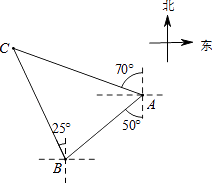
A.10 ![]() 海里
海里
B.10 ![]() 海里
海里
C.10 ![]() 海里
海里
D.20 ![]() 海里
海里
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读下面的内容,再解决问题.
例题:若m2+2mn+2n26n+9=0,求m和n的值.
解:∵m2+2mn+2n26n+9=0即:
∴m2+2mn+n2+n26n+9=0
∴![]()
∴即:m+n=0,n-3=0
∴m=3,n=3
(1)若![]() ,求
,求![]() 的值.
的值.
(2)若三角形三边a,b,C都是正整数,且满足![]() ,判断三角形的形状.
,判断三角形的形状.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,OE把∠BOD分成两部分;
(1)直接写出图中∠AOC的对顶角为 ,∠BOE的邻补角为 ;
(2)若∠AOC=70°,且∠BOE:∠EOD=2:3,求∠AOE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我县某初中为了创建书香校园,购进了一批图书.其中的20本某种科普书和30本某种文学书共花了1080元,经了解,购买的科普书的单价比文学书的单价多4元.
(1)购买的科普书和文学书的单价各多少元?
(2)另一所学校打算用800元购买这两种图书,问购进25本文学书后至多还能购进多少本科普书?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com