练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】若x=2019567891×2019567861，y=2019567881×2019567871，则x__y（填＞，＜或=）.

    【答案】<

    【解析】

    注意到四大数之间的关系，设2019567861=a，则2019567871=a+10，设2019567881=b，则2019567891＝b+10，根据代数式的运算法则比较x -y的结果即可..

    设2019567861=a，则2019567871=a+10

    设2019567881=b，则2019567891＝b+10

    x=2019567891×2019567861=a(b+10)=ab+10a

    y=2019567881×2019567871=b(a+10)=ab+10b

    x -y= ab+10a-( ab+10b)

    =10(a-b)

    =10(2019567861-2019567881)<0

    故答案为：<

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】据调查，某班20位女同学所穿鞋子的尺码如下表所示，则鞋子尺码的众数和中位数分别是（ ）

    尺码（码）

    34

    35

    36

    37

    38

    人数

    2

    5

    10

    2

    1


    A. 35码，35码
    B.35码，36码
    C.36码，35码
    D.36码，36码

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】包装厂有工人42人，每个工人平均每小时可以生产圆形铁片60片或长方形铁片40片，每两张圆形铁片和一张长方形铁片可配成一个密封圆桶，问如何安排工人才能使每小时生产的圆形铁片和长方形铁片能正好配套？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某班将买一些羽毛球和羽毛球拍，现了解情况如下：甲乙两家出售同样品牌的羽毛球和羽毛球拍，羽毛球拍每副定价64元，羽毛球每盒18元，经洽谈后，甲店每买一副羽毛球拍赠一盒羽毛球，乙店全部按定价的9折优惠，该班急需羽毛球拍6副，羽毛球x盒（不少于6盒）．

    （1）用代数式表示去甲、乙两店购买所需的费用；

    （2）当需要50盒羽毛球时，通过计算，说明此时去哪家购买较为合算；

    （3）当需要50盒羽毛球时，你能给出一种更为省钱的方法吗?试写出你的购买方法和所需的费用.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】2019年寒假即将到来，哈尔滨实验学校准备组织七年级学生参观冰雪大世界.参观门票学生票价为160元；冰雪大世界经营方为学校活动推出两种优惠方案，方案一：“所有学生门票一律九折”。方案二：“若学生人数超过100人，则超出的部分打八折”。

    （1）设学校有学生x人，用x分别表示方案一和方案二的费用.

    （2）学校为了能使学生安全快捷到达冰雪大世界，现准备集体租车去冰雪大世界，若单独租45座的客车若干辆，则有15人没有座位：若租同样数量60座的客车，则多出一辆，且其余客车恰好坐满，求七年级学生有多少人参观冰雪大世界；

    （3）在（2）的条件下，学校采用哪种优惠方案购买门票省钱，门票费用最低是多少.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商场销售一批名牌衬衫，平均每天可销售20件，每件赢利40元.为了扩大销售，增加赢利，商场决定采取适当降价措施.经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件.

    (1)若该商场平均每天要赢利1200元，且让顾客尽可能得到实惠，每件衬衫应降价多少元?

    (2)求该商场平均每天赢利的最大值。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为了加强公民的节水意识，合理利用水资源，某市采用价格调控的手段达到节水的目的，某市自来水收费的价目表如下（水费按月结算，m3表示立方米）

    价目表

    每月用水量

    价格

    不超过6m3的部分

    3元/m3

    超过6m3不超过10m3的部分

    5元/m3

    超过10m3的部分

    8元/m3

    根据上表的内容解答下列问题：

    （1）若小亮家1月份用水4m3，则应交水费　 　元；（直接写出答案，不写过程）;

    （2）若小亮家2月份用水am3（其中6＜a≤10），求小明家2月份应交水费多少元？（用含a的式子表示，写出过程并化简）;

    （3）若小亮家3月份交水费62元，求小亮家3月份的用水量是多少m3.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校抽查了某班级某月10天的用电量，数据如下表（单位：度）：

    度数

    8

    9

    10

    13

    14

    15

    天数

    1

    1

    2

    3

    1

    2

    （1）这10天用电量的众数是 ，中位数是 ，极差是 ；

    （2）求这个班级平均每天的用电量；

    （3）已知该校共有20个班级，该月共计30天，试估计该校该月总的用电量.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．

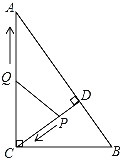
    （1）求线段CD的长；

    （2）当t为何值时，△CPQ与△ABC相似？

    （3）当t为何值时，△CPQ为等腰三角形？

    查看答案和解析>>

    同步练习册答案