练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】振华书店准备购进甲、乙两种图书进行销售，若购进本甲种图书和本乙种图书共需元，若购进本甲种图书和本乙种图书共需元.

    求甲、乙两种图书每本进价各多少元；

    该书店购进甲、乙两种图书共本进行销售，且每本甲种图书的售价为元，每本乙种图书的售价为元，如果使本次购进图书全部售出后所得利润不低于元，那么该书店至少需要购进乙种图书多少本？

    【答案】（1）30；（2）70

    【解析】

    （1）设每本甲种图书的进价为元，每本乙种图书的进价为元，得，解方程组可得；（2）设该书店购进乙种图书本，购机甲种图书本.根据题意，得，解不等式组可得.

    （1）解：设每本甲种图书的进价为元，每本乙种图书的进价为元.

    根据题意 得解得：

    答：每本甲种图书的进价为元，每本乙种图书的进价为元.

    （2）解：设该书店购进乙种图书本，购机甲种图书本.

    根据题意 得

    解得

    答：该书店至少购进乙图书本.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

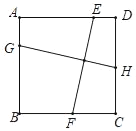
    【题目】如图在正方形ABCD中，E，F，G，H分别是AD，DC，BC，CD上的点，连接EF，GH．

    ①若EF⊥GH，则必有EF=GH．

    ②若EF=GH，则必有EF⊥GH．

    判断上述两个命题是否成立，若成立，请说明理由；若不成立，请举出反例．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，矩形OABC的顶点A、B在双曲线y= (x＞0)上，BC与x轴交于点D．若点A的坐标为(1，2)，则点B的坐标为_________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

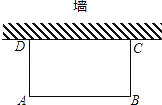
    【题目】如图，利用一面墙(墙的长度不超过45m)，用80m长的篱笆围一个矩形场地．

    (1)怎样围才能使矩形场地的面积为750m2？

    (2)能否使所围矩形场地的面积为810m2 ，为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

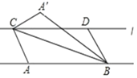
    【题目】如图，已知直线∥AB，与 AB 之间的距离为 2 ，C、D 是直线上两个动点（点 C在 D 点的左侧），且 AB=CD=5．连接 AC、BC、BD，将△ABC 沿 BC 折叠得到△A′BC．若以 A′、C、B、D 为顶点的四边形为矩形，则此矩形相邻两边之和为____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，将正方形OABC绕点O逆时针旋转45°后得到正方形OA1B1C1，依此方式，绕点O连续旋转2019次得到正方形OA2019B2019C2019，如果点A的坐标为(1，0)，那么点B2019的坐标为( )

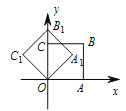
    A.(1，1)B.(0，)C.(-，0)D.(-1，1)

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】(1)问题发现

    在△ABC中，AC=BC，∠ACB=α，点D为直线BC上一动点，过点D作DF∥AC交AB于点F，将AD绕点D顺时针旋转α得到ED，连接BE．

    如图(1)，当α=90°时，试猜想：

    ①AF与BE的数量关系是　 　；②∠ABE=　 　；

    (2)拓展探究

    如图(2)，当0°<α<90°时，请判断AF与BE的数量关系及∠ABE的度数，并说明理由．

    (3)解决问题

    如图(3)，在△ABC中，AC=BC，AB=8，∠ACB=α，点D在射线BC上，将AD绕点D顺时针旋转α得到ED，连接BE，当BD=3CD时，请直接写出BE的长度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系xOy中，反比例函数y＝的图象与一次函数y＝k(x－2)的图象交点为A(3，2)，B(x，y)．

    (1)求反比例函数与一次函数的解析式及B点坐标；

    (2)若C是y轴上的点，且满足△ABC的面积为10，求C点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】 问题：如图1，在四边形ADBC中，∠ACB=∠ADB=90°，AD=BD，AC=，BC=2，求CD的长．

    （1）发现：张强同学解决这个问题的思路是：将△BCD绕点D逆时针旋转90°到△AED处，点B，C分别落在点A，E处（如图2），易证点C，A，E在同一条直线上，并且△CDE是等腰直角三角形，所以CE=CD，从而得到了AC，BC，CD三条线段之间的关系为：AC+BC=CD，从而求出CD的长是______ ；

    （2）应用：如图3，AB是⊙O的直径，点C，D在⊙O上，且，若AB=5，BC=4，求CD的长；

    （3）拓展：如图4，∠ACB=90°，AC=BC=2，点P为AB的中点，若点E满足CE=CA，点Q为AE的中点，直接写出线段PQ的长是______．

    查看答案和解析>>

    同步练习册答案