
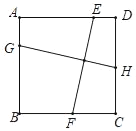
【题目】如图在正方形ABCD中,E,F,G,H分别是AD,DC,BC,CD上的点,连接EF,GH.
①若EF⊥GH,则必有EF=GH.
②若EF=GH,则必有EF⊥GH.
判断上述两个命题是否成立,若成立,请说明理由;若不成立,请举出反例.
【答案】①②两个命题成立;理由见解析.
【解析】
①作GM⊥CD于M,FN⊥AD于N,证明△EFN≌△HGM(ASA),即可得出EF=GH;
②作GM⊥CD于M,FN⊥AD于N,证明Rt△EFN≌Rt△HGM(HL),得出∠OGQ=∠PFQ,证出∠PQF+∠PFQ=90°,即可得出结论.
上述两个命题成立.理由如下:
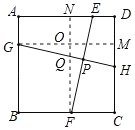
①作GM⊥CD于M,FN⊥AD于N,如图所示,则∠GMH=∠FNE=90°.
∵ABCD是正方形,
∴∠A=∠D=90°.
∴ADMG是矩形,
∴GM=AD,
同理可证:NFCD是矩形,
∴NF=DC.
∵四边形ABCD是正方形,
∴AD=DC,
∴FN=GM.
∵∠FND=∠D=∠GMD=90°,
∴∠MON=90°,
∴∠GOF=∠MON=90°,
∴∠OGQ+∠OQG=90°.
∵EF⊥GH,
∴∠PFQ+∠PQF=90°.
∵∠OQG=∠PQF,
∴∠OGQ=∠PFQ.
在△EFN和△HGM中,∵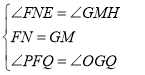 ,
,
∴△EFN≌△HGM(ASA),
∴EF=GH;
②作GM⊥CD于M,FN⊥AD于N,如图所示,则∠GMH=∠FNE=90°.
∵ABCD是正方形,
∴∠A=∠D=90°.
∴ADMG是矩形,
∴GM=AD,
同理可证:NFCD是矩形,
∴NF=DC.
∵四边形ABCD是正方形,
∴AD=DC,
∴FN=GM.
在Rt△EFN和Rt△HGM中,∵![]() ,
,
∴Rt△EFN≌Rt△HGM(HL),
∴∠OGQ=∠PFQ.
∵∠OGQ+∠OQG=90°,∠OQG=∠PQF,
∴∠PQF+∠PFQ=90°,
∴∠FPQ=90°,
∴EF⊥GH.


科目:初中数学 来源: 题型:
【题目】某宾馆有50个房间供游客住宿,当每个房间的房价为每天180元时,房间会全部住满.当每个房间 每天的房价每增加10元时,就会有一个房间空闲.宾馆需对游客居住的每个房间每天支出20元的各种费用.根据规定,每个房间每天的房价不得高于340元.设每个房间的房价增加x元(x为10的正整数倍).
(1)设一天订住的房间数为y,直接写出y与x的函数关系式及自变量x的取值范围;
(2)设宾馆一天的利润为w元,求w与x的函数关系式;
(3)一天订住多少个房间时,宾馆的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程![]()
(1)求证:方程总有两个不相等的实数根。
(2)m为何整数时,此方程的两个根都是正整数?
(3)若△ABC的两边AB,AC的长是这个方程的两个实数根,第三边BC的长为5,当△ABC是等腰三角形时,求m的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,矩形OABC的边OC在y轴上,边OA在x轴上,C点坐标为(0,3),点D是线段OA上的一个动点,连结CD,以CD为边作矩形CDEF,使边EF过点B.连结OF,当点D与点A重合时,所作矩形CDEF的面积为12.在点D的运动过程中,当线段OF有最大值时,则点F的坐标为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知二次函数经过点B(3,0),C(0,3),D(4,-5)

(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)若P是抛物线上一点,且S△ABP=![]() S△ABC,这样的点P有几个请直接写出它们的坐标.
S△ABC,这样的点P有几个请直接写出它们的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
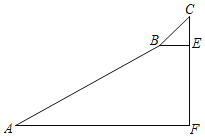
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每段山坡近似是“直”的,测得坡长AB=800米,BC=200米,坡角∠BAF=30°,坡角∠CBE=45°,则山峰的高度为( )米.
A.500B.400+100![]() C.
C.![]() D.541
D.541
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】振华书店准备购进甲、乙两种图书进行销售,若购进![]() 本甲种图书和
本甲种图书和![]() 本乙种图书共需
本乙种图书共需![]() 元,若购进
元,若购进![]() 本甲种图书和
本甲种图书和![]() 本乙种图书共需
本乙种图书共需![]() 元.
元.
![]() 求甲、乙两种图书每本进价各多少元;
求甲、乙两种图书每本进价各多少元;
![]() 该书店购进甲、乙两种图书共
该书店购进甲、乙两种图书共![]() 本进行销售,且每本甲种图书的售价为
本进行销售,且每本甲种图书的售价为![]() 元,每本乙种图书的售价为
元,每本乙种图书的售价为![]() 元,如果使本次购进图书全部售出后所得利润不低于
元,如果使本次购进图书全部售出后所得利润不低于![]() 元,那么该书店至少需要购进乙种图书多少本?
元,那么该书店至少需要购进乙种图书多少本?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com