
【题目】如图,在平面直角坐标系中,已知矩形OABC的顶点B(6,8),动点M,N同时从O点出发,点M沿射线OA方向以每秒1个单位的速度运动,点N沿线段OB方向以每秒0.6个单位的速度运动,当点N到达点B时,点M,N同时停止运动,连接MN,设运动时间为t(秒).
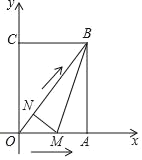
(1)求证△ONM~△OAB;
(2)当点M是运动到点![]() 时,若双曲线
时,若双曲线![]() 的图象恰好过点N,试求k的值;
的图象恰好过点N,试求k的值;
(3)△MNB与△OAB能否相似?若能试求出所有t的值,若不能请说明理由.
【答案】(1)见解析;(2)k=12;(3)能,t=6s或![]() s时,△BMN与△AOB相似.
s时,△BMN与△AOB相似.
【解析】
(1)用含t的式子表示OM,ON,可证得![]() ,即可解决问题;
,即可解决问题;
(2)根据M点坐标可求得运动时间,进而求得N点坐标,再利用待定系数法求解析式即可解决问题;
(3)分两种情形解决)①当点M与点A重合时,△BNM∽△BAO,此时求得t.②当OM=BM时,△MBN∽△BOA,此时点M在线段OB 的垂直平分线上,可求得此时t值
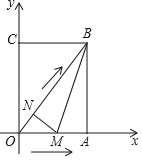
解:(1)证明:由题意:OA=6,AB=8,OB=10,OM=t,ON=0.6t,
∴![]() ,
,
∵∠MON=∠AOB,
∴△ONM∽△OAB.
(2)当OM=![]() 时,ON=5,
时,ON=5,
∴ON=NB,
∴N(3,4),
∵双曲线![]() 的图象恰好过点N,
的图象恰好过点N,
∴k=12.
(3)①当点M与点A重合时,△BNM∽△BAO,此时t=6s.
②当OM=BM时,∠MBN=∠AOB,∵∠OAB=∠MNB=90°,
∴△MBN∽△BOA,
此时点M在线段OB 的垂直平分线上,
由(2)可知,此时OM=![]() ,t=
,t=![]() s,
s,
综上所述,当t=6s或![]() s时,△BMN与△AOB相似.
s时,△BMN与△AOB相似.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:初中数学 来源: 题型:
【题目】若点(﹣2,y1)、(﹣1,y2)和(1,y3)分别在反比例函数y=﹣![]() 的图象上,则下列判断中正确的是( )
的图象上,则下列判断中正确的是( )
A. y1<y2<y3 B. y3<y1<y2 C. y2<y3<y1 D. y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把所有正偶数从小到大排列,并按如下规律分组:
第一组:2,4;
第二组:6,8,10,12;
第三组:14,16,18,20,22,24
第四组:26,28,30,32,34,36,38,40
……
则现有等式Am=(i,j)表示正偶数m是第i组第j个数(从左到右数),如A10=(2,3),则A2018=( )
A. (31,63) B. (32,17) C. (33,16) D. (34,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两家绿化养护公司各自推出了校园绿化养护服务的收费方案.
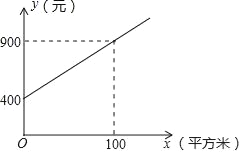
甲公司方案:每月的养护费用y(元)与绿化面积x(平方米)的关系如图所示.
乙公司方案:绿化面积不超过1000平方米时,每月收取费用5500元;绿化面积超过1000平方米时,超过的部分每月每平方米加收4元.
(1)求如图所示的y与x的函数表达式;
(2)如果某学校目前的绿化面积是1200平方米.那么选择哪家公司的服务比较划算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上点A表示数字6,点B表示数字﹣4
(1)画数轴,并在数轴上标出点A与点B;
(2)数轴上一动点C从点A出发,沿数轴的负方向以每秒2个单位长度的速度移动,经过4秒到达点E,数轴上另一动点D从点B出发,沿数轴的正方向以每秒1个单位长度的速度移动,经过8秒到达点F,求出点E与点F所表示的数,并在第(1)题的数轴上标出点E,点F;
(3)在第(2)题的条件下,在数轴上找出点H,使点H到点E距离与点H到点F距离之和为8,请在数轴上直接标出点H.(不需写出求解过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】江津区某玩具商城在“六一”儿童节来临之际,以49元/个的价格购进某种玩具进行销售,并预计当售价为50元/个时,每天能售出50个玩具,且在一定范围内,当每个玩具的售价平均每提高0.5元时,每天就会少售出3个玩具。
(1)若玩具售价不超过60元/个,每天售出玩具总成本不高于686元,预计每个玩具售价的取值范围;
(2)在实际销售中,玩具城以(1)中每个玩具的最低售价及相应的销量为基础,进一步调整了销售方案,将每个玩具的售价提高了![]() %,从而每天的销售量降低了
%,从而每天的销售量降低了![]() %,当每天的销售利润为147元时,求a的值.
%,当每天的销售利润为147元时,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
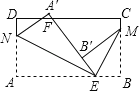
【题目】如图,长方形纸片ABCD,点E,F分别在边AB,CD上,连接EF.将∠BEF对折,点B落在直线EF上的点B′处,得折痕EM;将∠AEF对折,点A落在直线EF上的点A′处,得折痕EN.
(1)判断直线EN,ME的位置关系,并说明理由;
(2)设∠MEN的平分线EP交边CD于点P,∠MEN的一条三等分线EQ交边CD于点Q.求∠PEQ的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数![]() 的图象交于A(-4,n),B(2,-4)两点.
的图象交于A(-4,n),B(2,-4)两点.

(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)根据图象直接写出关于x的方程![]() 的解及不等式
的解及不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com