
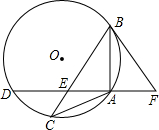
 如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.分析 (1)连接OB、OA或连接BD,由于AB=AC,则∠ABC=∠C,由AF=AE,则∠EBA=∠FBA,从而得出∠ABD+∠FBA=90°,即OB⊥BF,则BF是⊙O切线;
(2)由(1)得∠C=∠D,再由cos∠D=$\frac{4}{5}$,得$\frac{BD}{DF}$=$\frac{4}{5}$、$\frac{BF}{DF}$=$\frac{3}{5}$,从而求出BD.
(3)根据两三角形的高相同,它们的面积的比等于底边的比求解即可.
解答 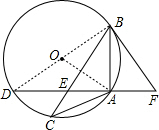 证明:(1)BF与⊙O相切,连接OB、OA,连接BD,
证明:(1)BF与⊙O相切,连接OB、OA,连接BD,
∵AD⊥AB,∴∠BAD=90°
∴BD是直径,∴BD过圆心
∵AB=AC,
∴∠ABC=∠C,
∵∠C=∠D,
∴∠ABC=∠D,
∵AD⊥AB,
∴∠ABD+∠D=90°,
∵AF=AE,
∴∠EBA=∠FBA,
∴∠ABD+∠FBA=90°,
∴OB⊥BF,
∴BF是⊙O切线(4分);
(2)∵∠C=∠D,cos∠C=$\frac{4}{5}$,
∴cos∠D=$\frac{4}{5}$,
∵BF=5,
∴$\frac{BD}{DF}$=$\frac{4}{5}$,
∴$\frac{BF}{DF}$=$\frac{3}{5}$,
∴BD=$\frac{4}{3}$×5=$\frac{20}{3}$,
∴直径为$\frac{20}{3}$;
(3)∵cos∠F=$\frac{3}{5}$,
∴cos∠BEA=$\frac{3}{5}$,
设AF=AE=3x,则BF=BE=5x、AB=AC=4x,
∴BD=$\frac{20}{3}x$,AD=$\frac{16x}{3}$,
∴DE=$\frac{7}{3}$x,
∵△ACE∽△BDE,
∴CE:DE=AE:BE,
∴CE=$\frac{7}{5}$x,
∴$\frac{{{S_{△ACE}}}}{{{S_{△ABE}}}}$=$\frac{CE}{BE}$=$\frac{\frac{7}{5}x}{5}$=$\frac{7}{25}$.
点评 此题考查了切线的判定方法相似三角形的判定级性质及圆的综合知识,运用了三角函数求线段的长,综合性较强,难度偏大.


科目:初中数学 来源: 题型:选择题
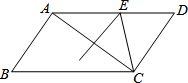 如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )
如图,在平行四边形ABCD中,AB=8,BC=12,AC的垂直平分线交AD于点E,则△CDE的周长是( )| A. | 14 | B. | 20 | C. | 22 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.
菱形ABCD中,对角线AC,BD交于点O,BE⊥AD交AC于F,AF=BD,G为BD上的点,EG∥AB.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
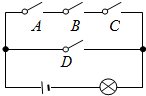 如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )
如图,电路图上有四个开关A、B、C、D和一个小灯泡,闭合开关D或同时闭合开关A、B、C都可使小灯泡发光,则任意闭合其中两个开关,小灯泡发光的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{2}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{2}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
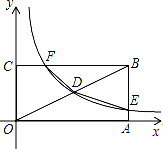 如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )
如图,矩形OABC的顶点A、C分别在x、y的正半轴上,点D为对角线OB的中点,反比例函数y=$\frac{k}{x}$在第一象限内的图象经过点D,且与AB、BC分别交于E、F两点,若四边形BEDF的面积为4.5,则k的值为( )| A. | 2 | B. | 3 | C. | 6 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源:2016-2017学年江苏省南通市七年级3月月考数学试卷(解析版) 题型:单选题
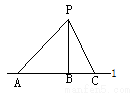
如图,P为直线l外一点,A、B、C在l上,且PB⊥l,下列说法中,正确的个数是( )
①PA、PB、PC三条线段中,PB最短
②线段PB的长叫做点P到直线l的距离
③线段AB是点A到PB的距离
④线段AC的长是点A到PC的距离
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com