练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，EF过□ABCD对角线的交点O，交AD于E，交BC于F，若□ ABCD的周长为16，OE＝2.5，则四边形EFCD的周长为(　　)

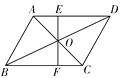
    A. 10 B. 11 C. 12 D. 13

    【答案】D

    【解析】分析：先利用平行四边形的性质求出AB=CD，BC=AD，AD+CD=9，可利用全等的性质得到△AEO≌△CFO，求出OE=OF=1.5，即可求出四边形的周长．

    详解：∵四边形ABCD是平行四边形，周长为16，

    ∴AB=CD，BC=AD，OA=OC，AD∥BC，

    ∴CD+AD=8，∠OAE=∠OCF，

    在△AEO和△CFO中，

    ，

    ∴△AEO≌△CFO（ASA），

    ∴OE=OF=2.5，AE=CF，

    则EFCD的周长=ED+CD+CF+EF=（DE+CF）+CD+EF=AD+CD+EF=8+5=13．

    故选D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】（1）填空：

    （a﹣b）（a+b）=　 　

    （a﹣b）（a2+ab+b2）=　 　

    （a﹣b）（a3+a2b+ab2+b3）=　 　

    （2）猜想：（a﹣b）（an﹣1+an﹣2b+…+abn﹣2+bn﹣1）=　 　（其中n为正整数，且n≥2）．

    （3）利用（2）猜想的结论计算：39﹣38+37﹣…+33﹣32+3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下列是用火柴棒拼出的一列图形．

    仔细观察，找出规律，解答下列各题：

    （1）第6个图中共有　 　根火柴；

    （2）第n个图形中共有　 　根火柴（用含n的式子表示）

    （3）第2017个图形中共有多少根火柴？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l与⊙O交于C，D两点，且与半径OA垂直，垂足为H，∠ODC=30°，在OD的延长线上取一点B，使得AD=BD，若⊙O的半径为2，则图中阴影部分的面积为（结果保留π）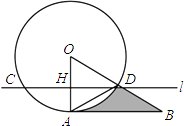

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，半径为1个单位的圆片上有一点A与数轴上的原点重合，AB是圆片的直径．(注：结果保留π )

    (1)把圆片沿数轴向右滚动半周，点B到达数轴上点C的位置，点C表示的数是　 　数(填“无理”或“有理”)，这个数是　 　；

    (2)把圆片沿数轴滚动2周，点A到达数轴上点D的位置，点D表示的数是　 　；

    (3)圆片在数轴上向右滚动的周数记为正数，圆片在数轴上向左滚动的周数记为负数，依次运动情况记录如下：+2，﹣1，+3，﹣4，﹣3．

    ①第　 　次滚动后，A点距离原点最近，第　 　次滚动后，A点距离原点最远．

    ②当圆片结束运动时，A点运动的路程共有　 　，此时点A所表示的数是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，对角线AC，BD相交于点O，过点D作对角线BD的垂线交BA的延长线于点E.

    （1）证明：四边形ACDE是平行四边形；

    （2）若AC＝4，BD＝3，求△ADE的周长

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB是⊙O的直径，点C，D是半圆O的三等分点，过点C作⊙O的切线交AD的延长线于点E，过点D作DF⊥AB于点F，交⊙O于点H，连接DC，AC．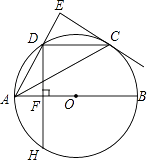
    （1）求证：∠AEC=90°；
    （2）试判断以点A，O，C，D为顶点的四边形的形状，并说明理由；
    （3）若DC=2，求DH的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1是某班学生上学的三种方式（乘车、步行、骑车）的人数分布直方图和扇形图2．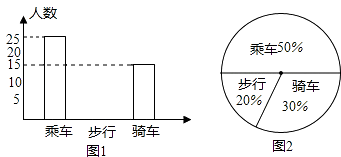
    （1）该班有多少名学生；
    （2）补上人数分布直方图的空缺部分；
    （3）若全年级有800人，估计该年级步行有名学生．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，点A，B的坐标分别为（﹣1，0），（3，0），现同时将点A，B分别向上平移2个单位，再向右平移1个单位，分别得到点A，B的对应点C，D，连接AC，BD，CD．得平行四边形ABDC

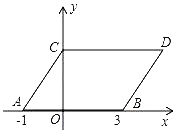
    （1）直接写出点C，D的坐标；

    （2）若在y轴上存在点 M，连接MA，MB，使S△MAB=S平行四边形ABDC ， 求出点M的坐标．

    （3）若点P在直线BD上运动，连接PC，PO．

    请画出图形，直接写出∠CPO、∠DCP、∠BOP的数量关系．

    查看答案和解析>>

    同步练习册答案