
【题目】如图,直线l与⊙O交于C,D两点,且与半径OA垂直,垂足为H,∠ODC=30°,在OD的延长线上取一点B,使得AD=BD,若⊙O的半径为2,则图中阴影部分的面积为(结果保留π) 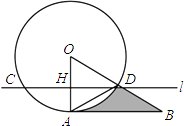
【答案】2 ![]() ﹣
﹣ ![]() π
π
【解析】解:直线AB与⊙O的位置关系是相切, 理由是:∵AO⊥CD,
∴∠OAD=90°,
∵∠ODC=30°,
∴∠DOA=60°,
∵OA=OD,
∴△OAD是等边三角形,
∴∠OAD=∠ODA=60°,
∵AD=BD,
∴∠DAB=∠B,
∵∠ODA=∠B+∠DAB,
∴∠DAB=∠B=30°,
∴∠OAB=30°+60°=90°,
∵∠B=30°,∠OAB=90°,OA=2,
∴OB=2OA=4,由勾股定理得:AB=2 ![]() ,
,
∴阴影部分的面积S=S△OAB﹣S扇形OAD= ![]() ×2
×2 ![]() ×2﹣
×2﹣ ![]() =2
=2 ![]() ﹣
﹣ ![]() π.
π.
所以答案是:2 ![]() ﹣
﹣ ![]() π.
π.
【考点精析】掌握扇形面积计算公式是解答本题的根本,需要知道在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】为响应绿色出行号召,越来越多市民选择租用共享单车出行,已知某共享单车公司为市民提供了手机支付和会员卡支付两种支付方式,如图描述了两种方式应支付金额y(元)与骑行时间x(时)之间的函数关系,根据图象回答下列问题:
(1)求手机支付金额y(元)与骑行时间x(时)的函数关系式;
(2)李老师经常骑行共享单车,请根据不同的骑行时间帮他确定选择哪种支付方式比较合算.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平价商场经销甲、乙两种商品,甲种商品每件售价60元,利润率为50%;乙种商品每件进价50元,售价80元.
(1)每件甲种商品的进价为 元,每件乙种商品的利润率为 ;
(2)若该商场同时购进甲、乙两种商品共50件,恰好总进价为2100元,求购进甲种商品多少件.
(3)在元旦期间,该商场只对甲、乙两种商品进行如下的优惠促销活动:

按上述优惠条件,若小华一次性购买乙种商品实际付款504元,求小华在该商场购买乙种商品多少件.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】蜗牛从某点![]() 开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):
开始沿一东西方向直线爬行,规定向东爬行的路程记为正数,向西爬行的路程记为负数.爬过的各段路程依次为(单位:厘米):![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 通过计算说明蜗牛是否回到起点
通过计算说明蜗牛是否回到起点![]() .
.
![]() 蜗牛离开出发点
蜗牛离开出发点![]() 最远时是多少厘米?
最远时是多少厘米?
![]() 在爬行过程中,如果每爬
在爬行过程中,如果每爬![]() 厘米奖励
厘米奖励![]() 粒芝麻,则蜗牛一共得到多少粒芝麻?
粒芝麻,则蜗牛一共得到多少粒芝麻?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,直线AB与x轴交于点A,与y轴交于点B,点A的坐标为(3,0),点B的坐标为(0,4),点P为双曲线y= ![]() (x>0)上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,ADBC的值为
(x>0)上的一点,过点P分别作x轴、y轴的垂线段PE、PF,当PE、PF分别与线段AB交于点C、D时,ADBC的值为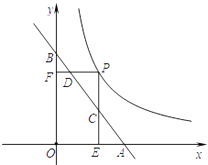
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,EF过□ABCD对角线的交点O,交AD于E,交BC于F,若□ ABCD的周长为16,OE=2.5,则四边形EFCD的周长为( )
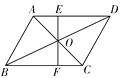
A. 10 B. 11 C. 12 D. 13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“端午节”所示我国的传统佳节,民间历来有吃“粽子”的习俗,我市某食品厂为了解市民对去年销售较好的肉馅棕、豆沙馅粽、红枣馅粽、蛋黄馅粽(以下分别用A、B、C、D表示)这四种不用口味粽子的喜爱情况,在节前对某居民区进行了抽样调查,并将调查情况绘制成如下两幅统计图(尚不完整). 
请根据以上信息回答:
(1)本次参加抽样调查的居民有多少人?
(2)将两幅不完整的图补充完整;
(3)若居民区有8000人,请估计爱吃D粽的人数;
(4)若有外型完全相同的A、B、C、D粽各一个,煮熟后,小王吃了两个,用列表或画树状图的方法,求他第二个恰好吃到的是C粽的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com