【题目】如图，四边形
是正方形，
是
边所在直线上的点，
，且
交正方形外角
的平分线
于点
.
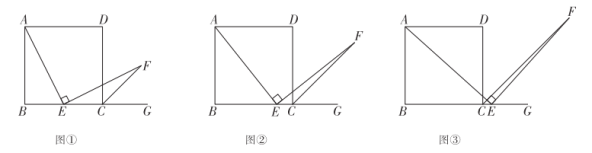
（1）当点在线段中点时（如图①），易证
，不需证明；
（2）当点在线段上（如图②）或在线段延长线上（如图③）时，（1）中的结论是否仍然成立？请写出你的猜想，并选择图②或图③的一种结论给予证明.
【答案】（1）见解析；（2）成立，理由见解析.
【解析】
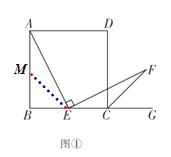
（1）图①在AB上取一点M，使AM=EC，连接ME，证明△AME≌△BCF，从而可得到AE=EF；
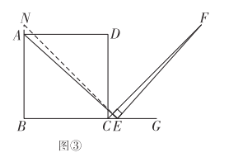
（2）图②在AB上取一点M，使AM=EC，连接ME，证明△AME≌△BCF，从而可得到AE=EF；图③在BA的延长线上取一点N，使AN=CE，连接NE，然后证明△ANE≌△ECF，从而可得到AE=EF．
解：在
上取一点
，使
，连接
.
∴
.
∴
.
∴
.
∵
是外角
的平分线，
∴
.
∴
.
∴
.
∵
，
，
∴
.
∴
.
∴
.
（2）图②结论：.图③结论：.
图②证明：如图②，在上取一点，使，连接.
∴.
∴.
∴.
∵是外角的平分线，
∴.
∴.
∴.
∵，，
∴.
∴.
∴.
图③证明：如图③，在
的延长线上取一点
，使
，连接
.
∴
.
∴
.
∵四边形
是正方形，
∴
.
∴
.
∴
.
∴
.
∴.
科目：初中数学 来源： 题型：
【题目】下列是用火柴棒拼成的一组图形，第①个图形中有 3 根火柴棒，第②个图形中有 9 根火柴棒，第③个图形中有 18 根火柴棒，…，按此规律排列下去，第⑥个图形中火柴棒的根数是（ ）.
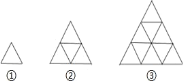
A. 63B. 60C. 56D. 45
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，E是AD上一点，PQ垂直平分BE，分别交AD、BE、BC于点P、O、Q，连接BP、EQ．
（1）求证：四边形BPEQ是菱形；
（2）若AB=6，F为AB的中点，OF+OB=9，求PE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图所示，在正方形
中，边长为2的等边三角形
的顶点
，
分别在
和
上.下列结论：①
；②
；③
；④
.其中结论正确的序号是（ ）
A. ①②③B. ①②④C. ①③④D. ②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】甲、乙两校的学生人数基本相同，为了解这两所学校学生的数学学业水平，在同一次测试中，从两校各随机抽取了30名学生的测试成绩进行调查分析，其中甲校已经绘制好了条形统计图，乙校只完成了一部分．
甲校 93 82 76 77 76 89 89 89 83 87 88 89 84 92 87
89 79 54 88 92 90 87 68 76 94 84 76 69 83 92
乙校 84 63 90 89 71 92 87 92 85 61 79 91 84 92 92
73 76 92 84 57 87 89 88 94 83 85 80 94 72 90
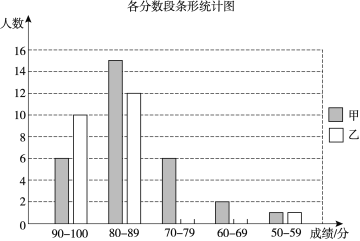
（1）请根据乙校的数据补全条形统计图；
（2）两组样本数据的平均数、中位数、众数如下表所示，请补全表格；
平均数 | 中位数 | 众数 | |
甲校 | 83.4 | 87 | 89 |
乙校 | 83.2 |
（3）两所学校的同学都想依据抽样的数据说明自己学校学生的数学学业水平更好一些，
请为他们各写出一条可以使用的理由；
甲校： ．乙校： ．
（4）综合来看，可以推断出 校学生的数学学业水平更好一些，理由为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
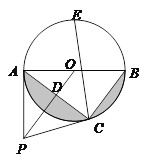
【题目】如图，点P是⊙O 外一点，PA切⊙O于点A，AB是⊙O的直径，连接OP，过点B作BC∥OP交⊙O于点C，连接AC交OP于点D．
(1)求证：PC是⊙O的切线；
(2)若PD=cm，AC=8cm，求图中阴影部分的面积；
(3)在(2)的条件下，若点E是
的中点，连接CE，求CE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知一次函数
的图象与二次函数
（
为常数）的图象交于
两点，且点
的坐标为
.
（1）求出
的值及点
的坐标；
（2）设
，若
时，
随着
的增大而增大，且
也随着的增大而增大，求
的最小值和
的最大值.
查看答案和解析>>
科目：初中数学 来源： 题型：
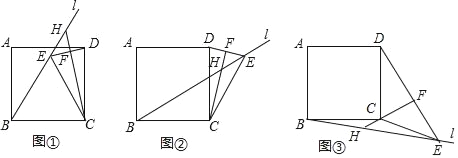
【题目】在正方形ABCD中，过点B作直线l，点E在直线l上，连接CE，DE，CE=BC，过点C作CF⊥DE于点F，交直线l于点H，当l在如图①的位置时，易证：BH+EH=
CH（不需证明）．
（1）当l在如图②的位置时，线段BH，EH，CH之间有怎样的数量关系？写出你的猜想，并给予证明；
（2）当l在如图③的位置时，线段BH，EH，CH之间有怎样的数量关系？写出你的猜想，不必证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
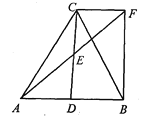
【题目】如图，在△ABC中，D是AB的中点，E是CD的中点， 过点C作CF//AB交AE的延长线于点F，连接BF．
(1) 求证：DB＝CF；
(2) 如果AC＝BC，试判断四边形BDCF的形状，并证明你的结论．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com