
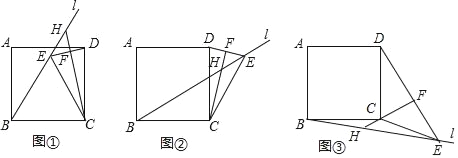
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌЙ§ЕуBзїжБЯпlЃЌЕуEдкжБЯпlЩЯЃЌСЌНгCEЃЌDEЃЌCE=BCЃЌЙ§ЕуCзїCFЁЭDEгкЕуFЃЌНЛжБЯпlгкЕуHЃЌЕБlдкШчЭМЂйЕФЮЛжУЪБЃЌвзжЄЃКBH+EH=![]() CHЃЈВЛашжЄУїЃЉЃЎ
CHЃЈВЛашжЄУїЃЉЃЎ
ЃЈ1ЃЉЕБlдкШчЭМЂкЕФЮЛжУЪБЃЌЯпЖЮBHЃЌEHЃЌCHжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПаДГіФуЕФВТЯыЃЌВЂИјгшжЄУїЃЛ
ЃЈ2ЃЉЕБlдкШчЭМЂлЕФЮЛжУЪБЃЌЯпЖЮBHЃЌEHЃЌCHжЎМфгадѕбљЕФЪ§СПЙиЯЕЃПаДГіФуЕФВТЯыЃЌВЛБижЄУїЃЎ
ЁОД№АИЁПЃЈ1ЃЉBHЉEH=![]() CHЃЈ2ЃЉEHЉBH=
CHЃЈ2ЃЉEHЉBH=![]() CH
CH
ЁОНтЮіЁПЗжЮі: ЃЈ1ЃЉЯШХаЖЯГіЁЯBCG=ЁЯECG=![]() ЁЯBCEЃЌдйХаЖЯГіЁЯECF=ЁЯDCF=
ЁЯBCEЃЌдйХаЖЯГіЁЯECF=ЁЯDCF=![]() ЁЯDCEЃЌЕУГіЁЯGCH=ЁЯGCE-ЁЯECF=
ЁЯDCEЃЌЕУГіЁЯGCH=ЁЯGCE-ЁЯECF=![]() ЃЈЁЯBCE-ЁЯDCEЃЉ=45ЁуЃЌМДЃКЁїCGHЪЧЕШбќжБНЧШ§НЧаЮЃЌНјЖјЕУГіCH=
ЃЈЁЯBCE-ЁЯDCEЃЉ=45ЁуЃЌМДЃКЁїCGHЪЧЕШбќжБНЧШ§НЧаЮЃЌНјЖјЕУГіCH=![]() GHНјЖјХаЖЯГіBG=EG=
GHНјЖјХаЖЯГіBG=EG=![]() BEМДПЩЕУГіНсТлЃЛ
BEМДПЩЕУГіНсТлЃЛ
ЃЈ2ЃЉЭЌЃЈ1ЃЉЕФЗНЗЈМДПЩЕУГіНсТлЃЎ
ЯъНт:
ЃЈ1ЃЉBHЉEH=![]() CHЃЛ
CHЃЛ
РэгЩШчЯТЃК
Й§ЕуCзїCGЁЭBHгкGЃЌ
ШчЭМЂкЫљЪОЃЌ
ЁпЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
ЁрCB=CDЃЌЁЯBCD=90ЁуЃЌ
ЁпCE=CBЃЌ
ЁрЁЯBCG=ЁЯECG=![]() ЁЯBCEЃЌ
ЁЯBCEЃЌ
ЁпCEЁЭDEЃЌCD=CB=CEЃЌ
ЁрЁЯECF=ЁЯDCF=![]() ЁЯDCEЃЌ
ЁЯDCEЃЌ
ЁрЁЯGCH=ЁЯGCEЉЁЯECF=![]() ЃЈЁЯBCEЉЁЯDCEЃЉ=45Ёу
ЃЈЁЯBCEЉЁЯDCEЃЉ=45Ёу
ЁрЁїCGHЪЧЕШбќжБНЧШ§НЧаЮЃЌ
ЁрCH=![]() GHЃЌ
GHЃЌ
ЁпCB=CEЃЌCGЁЭBEЃЌ
ЁрBG=EG=![]() BEЃЌ
BEЃЌ
ЁрBHЉEH=BG+GHЉEH=BG+EGЉEHЉEH=2GH=![]() CH
CH
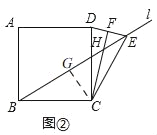
ЃЈ2ЃЉВТЯыЃКEHЉBH=![]() CHЃЌ
CHЃЌ
РэгЩЃКШчЭМЂлЃЌЙ§ЕуCзїCGЁЭBEгкGЃЌ
ЭЌЃЈ1ЃЉЕУЃЌЁїCGHЪЧЕШбќжБНЧШ§НЧаЮЃЌ
CH=![]() GHЃЌ
GHЃЌ
ЁпCB=CEЃЌCGЁЭBEЃЌ
ЁрBG=EG=![]() BEЃЌ
BEЃЌ
ЁрEHЉBH=HG+GEЉЃЈBGЉHGЃЉ=2HG=![]() CHЃЎ
CHЃЎ
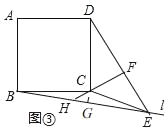
ЕуОІ: БОЬтЪЧЫФБпаЮзлКЯЬтЃЌжївЊПМВщСЫе§ЗНаЮЕФаджЪЁЂа§зЊЕФаджЪЁЂЕШбќШ§НЧаЮЕФаджЪЁЂЕШбќжБНЧШ§НЧаЮЕФХаЖЈгыаджЪЕШжЊЪЖЃЛЧѓГіЁЯGCH=45ЁуЪЧНтБОЬтЕФЙиМќ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
гаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎ
![]() ЧѓЪЕЪ§
ЧѓЪЕЪ§![]() ЕФШЁжЕЗЖЮЇЃЛ
ЕФШЁжЕЗЖЮЇЃЛ
![]() ЪЧЗёДцдкЪЕЪ§
ЪЧЗёДцдкЪЕЪ§![]() ЃЌЪЙЗНГЬЕФСНИіЪЕЪ§ИљжЎКЭЕШгкСНЪЕЪ§ИљжЎЛ§ЕФЫуЪѕЦНЗНИљЃПШєДцдкЃЌЧѓГі
ЃЌЪЙЗНГЬЕФСНИіЪЕЪ§ИљжЎКЭЕШгкСНЪЕЪ§ИљжЎЛ§ЕФЫуЪѕЦНЗНИљЃПШєДцдкЃЌЧѓГі![]() ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ЕФжЕЃЛШєВЛДцдкЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() ЪЧе§ЗНаЮЃЌ
ЪЧе§ЗНаЮЃЌ![]() ЪЧ
ЪЧ![]() БпЫљдкжБЯпЩЯЕФЕуЃЌ
БпЫљдкжБЯпЩЯЕФЕуЃЌ![]() ЃЌЧв
ЃЌЧв![]() НЛе§ЗНаЮЭтНЧ
НЛе§ЗНаЮЭтНЧ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() гкЕу
гкЕу![]() .
.
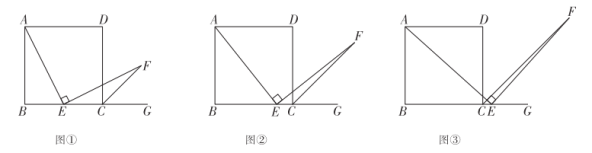
ЃЈ1ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() жаЕуЪБЃЈШчЭМЂйЃЉЃЌвзжЄ
жаЕуЪБЃЈШчЭМЂйЃЉЃЌвзжЄ![]() ЃЌВЛашжЄУїЃЛ
ЃЌВЛашжЄУїЃЛ
ЃЈ2ЃЉЕБЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЩЯЃЈШчЭМЂкЃЉЛђдкЯпЖЮ
ЩЯЃЈШчЭМЂкЃЉЛђдкЯпЖЮ![]() бгГЄЯпЩЯЃЈШчЭМЂлЃЉЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПЧыаДГіФуЕФВТЯыЃЌВЂбЁдёЭМЂкЛђЭМЂлЕФвЛжжНсТлИјгшжЄУї.
бгГЄЯпЩЯЃЈШчЭМЂлЃЉЪБЃЌЃЈ1ЃЉжаЕФНсТлЪЧЗёШдШЛГЩСЂЃПЧыаДГіФуЕФВТЯыЃЌВЂбЁдёЭМЂкЛђЭМЂлЕФвЛжжНсТлИјгшжЄУї.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
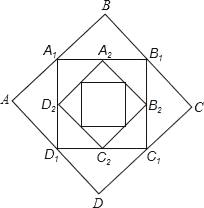
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ1ЃЌЫГДЮСЌНге§ЗНаЮABCDЫФБпЕФжаЕуЕУЕНЕквЛИіе§ЗНаЮA1B1C1D1ЃЌдйЫГДЮСЌНге§ЗНаЮA1B1C1D1ЫФБпЕФжаЕуЕУЕНЕкЖўИіе§ЗНаЮA2B2C2D2ЁЃЌвдДЫРрЭЦЃЌдђЕк2018Иіе§ЗНаЮA2018B2018C2018D2018ЕФжмГЄЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌаЁЯЭЮЊСЫЬхбщЫФБпаЮЕФВЛЮШЖЈадЃЌНЋЫФИљФОЬѕгУЖЄзгЖЄГЩвЛИіОиаЮПђМмABCDЃЌBгыDСНЕужЎМфгУвЛИљЯ№ЦЄНюРжБЙЬЖЈЃЌШЛКѓЯђгвХЄЖЏПђМмЃЌЙлВьЫљЕУЫФБпаЮЕФБфЛЏЃЌЯТСаХаЖЯДэЮѓЕФЪЧЃЈ ЃЉ
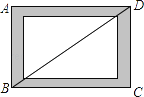
A. ЫФБпаЮABCDгЩОиаЮБфЮЊЦНааЫФБпаЮ B. BDЕФГЄЖШдіДѓ
C. ЫФБпаЮABCDЕФУцЛ§ВЛБф D. ЫФБпаЮABCDЕФжмГЄВЛБф
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
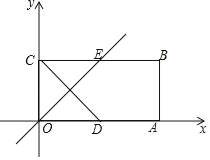
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌОиаЮOABCЕФЖЅЕуBЕФзјБъЮЊЃЈ4ЃЌ2ЃЉЃЌDЪЧOAЕФжаЕуЃЌOEЁЭCDНЛBCгкЕуEЃЌЕуPДгЕуOГіЗЂЃЌвдУПУы2ИіЕЅЮЛГЄЖШЕФЫйЖШбиЩфЯпOEдЫЖЏЃЎ
ЃЈ1ЃЉЧѓжБЯпOEЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЩшвдCЃЌPЃЌDЃЌBЮЊЖЅЕуЕФЭЙЫФБпаЮЕФУцЛ§ЮЊSЃЌЕуPЕФдЫЖЏЪБМфЮЊtЃЈЕЅЮЛЃКУыЃЉЃЌЧѓSЙигкtЕФКЏЪ§НтЮіЪНЃЌВЂаДГіздБфСПtЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉЩшЕуNЮЊОиаЮЕФжааФЃЌдђдкЕуPдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуPЃЌЪЙвдPЃЌCЃЌNЮЊЖЅЕуЕФШ§НЧаЮЪЧжБНЧШ§НЧаЮЃПШєДцдкЃЌЧыжБНгаДГіtЕФжЕМАЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ![]() ЃЌдк
ЃЌдк![]() жаЃЌ
жаЃЌ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() гы
гы![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌЭЈЙ§ЩЯЪіЬѕМўЃЌЮвУЧВЛФбЗЂЯжЃК
ЃЌЭЈЙ§ЩЯЪіЬѕМўЃЌЮвУЧВЛФбЗЂЯжЃК![]() ЃЛШчЭМ
ЃЛШчЭМ![]() ЃЌ
ЃЌ![]() ЕФЦНЗжЯп
ЕФЦНЗжЯп![]() гы
гы![]() ЕФЭтНЧЦНЗжЯп
ЕФЭтНЧЦНЗжЯп![]() ЯрНЛгк
ЯрНЛгк![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зї
зї![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ЃЌНЛжБЯп
ЃЌНЛжБЯп![]() гкЕу
гкЕу![]() ИљОнЭМ
ИљОнЭМ![]() ЫљЕУЕФНсТлЃЌЪдВТЯы
ЫљЕУЕФНсТлЃЌЪдВТЯы![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() жЎМфДцдкЪВУДЙиЯЕЃП( )
жЎМфДцдкЪВУДЙиЯЕЃП( )
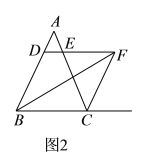
A. ![]() B.
B. ![]() C.
C. ![]() D. ЮоЗЈХаЖЯ
D. ЮоЗЈХаЖЯ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
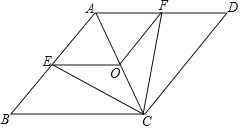
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкСтаЮABCDжаЃЌЕуEЃЌOЃЌFЗжБ№ЮЊABЃЌACЃЌADЕФжаЕуЃЌСЌНгCEЃЌCFЃЌOEЃЌOFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїBCEЁеЁїDCFЃЛ
ЃЈ2ЃЉЕБABгыBCТњзуЪВУДЙиЯЕЪБЃЌЫФБпаЮAEOFЪЧе§ЗНаЮЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
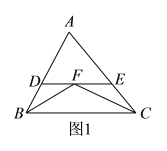
ЁОЬтФПЁПШчЭМЃЌЁїABCЕФУцЛ§ЮЊ8cm2ЃЌAPДЙжБЁЯBЕФЦНЗжЯпBPгкPЃЌдђЁїPBCЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
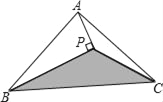
A. 2cm2 B. 3cm2 C. 4cm2 D. 5cm2
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com