
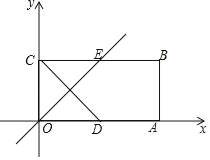
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�����OABC�Ķ���B������Ϊ��4��2����D��OA���е㣬OE��CD��BC�ڵ�E����P�ӵ�O��������ÿ��2����λ���ȵ��ٶ�������OE�˶���
��1����ֱ��OE�Ľ���ʽ��
��2������C��P��D��BΪ������ı��ε����ΪS����P���˶�ʱ��Ϊt����λ���룩����S����t�ĺ�������ʽ����д���Ա���t��ȡֵ��Χ��
��3�����NΪ���ε����ģ����ڵ�P�˶������У��Ƿ���ڵ�P��ʹ��P��C��NΪ�������������ֱ�������Σ������ڣ���ֱ��д��t��ֵ����P�����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y=x����2��S=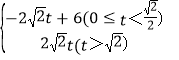 ����3�����ڣ� t=
����3�����ڣ� t=![]() ʱ��P��
ʱ��P��![]() ��
��![]() ����t=
����t=![]() ʱ��P��2��2����t=
ʱ��P��2��2����t=![]() ʱ��P��3��3����
ʱ��P��3��3����
������������: ��1���������COE=45�㣬�������CE=OC=2�����ɵó����ۣ�
��2���ֵ�P��OM����ME��OE���ӳ����ϣ���������ĺͲ�ɵó����ۣ�
��3����������������ù��ɶ��������������ʱ��t�����ɵó�����.
���:
��1��������ã�OD=OC=2��
��OE��CD��
��OEƽ�֡�COD��
���COE=![]() ��AOC=45�㣬
��AOC=45�㣬
��OC=CE=2��
��E��2��2������ֱ��OE�Ľ���ʽΪy=kx������E�������ã�2=2k��
��k=1��
��ֱ��OE�Ľ���ʽΪy=x��
��2����Rt��COE�У����ݹ��ɶ����ã�OE=2![]() ��
��
������ã��Ե�C��P��D��BΪ�����ͼ�����ı��Σ�
��t��![]() ��t
��t![]() ��
��
�����������
��OE��CD�Ľ���ΪM��
�ٵ���P��OM���˶�ʱ��0��t��![]() ��
��
S=S����OABC��S��POC��S��POD��S��DAB=8��![]() ��
��![]() ��2=��2
��2=��2![]() t+6��
t+6��
�ڵ���P��ME���˶�ʱ��![]() ��t��
��t��![]() ���Ե�C��P��D��BΪ������ı���Ϊ���ı��Σ����������⣬
���Ե�C��P��D��BΪ������ı���Ϊ���ı��Σ����������⣬
�۵�P��OE���ӳ������˶�ʱ��t��![]() ��
��
S=S��CDB+S��PCB=![]() =2
=2![]() t��
t��
S=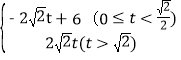 ��
��
��3�����ڣ����ɣ�PC2=��![]() t��2+��2��
t��2+��2��![]() t��2=4t2��4
t��2=4t2��4![]() t+4��PN2=��2��
t+4��PN2=��2��![]() t��2+��1��
t��2+��1��![]() t��2=4t2��6
t��2=4t2��6![]() t+5��NC2=5��
t+5��NC2=5��
�ٵ���CPN=90��ʱ��PC2+PN2=CN2��
��4t2��4![]() t+4+4t2��6
t+4+4t2��6![]() t+5=5��
t+5=5��
��t=![]() ��t=
��t=![]() ��
��
��P��![]() ��
��![]() ����2��2����
����2��2����
�ڵ���PNC=90��ʱ��CN2+PN2=PC2��
��5+4t2��6![]() t+5=4t2��4
t+5=4t2��4![]() t+4��
t+4��
��t=![]() ��
��
��P��3��3����
�۵���PCN=90��ʱ��PC2+CN2=PN2��4t2��4![]() t+4+5=4t2��6
t+4+5=4t2��6![]() t+5��
t+5��
��t=��![]() ����ʱ�����ڵ�P��
����ʱ�����ڵ�P��
����t=![]() ʱ��P��
ʱ��P��![]() ��
��![]() ����t=
����t=![]() ʱ��P��2��2����t=
ʱ��P��2��2����t=![]() ʱ��P��3��3����
ʱ��P��3��3����
�㾦: ������һ�κ����ۺ��⣬��Ҫ�����˽�ƽ���ߵ����ʣ�����ϵ����������ͼ�ε�����ļ��㷽�������ɶ��������ù��ɶ������������ǽⱾ��Ĺؼ�.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������ڴ�����ȫ��������������ijУ��ٰ�������֪ʶ����������������A��B���ֽ�Ʒ�Թ��������ߣ��������A��20����B��15��������380Ԫ���������A��15����B��10��������280Ԫ��
��1��A��B���ֽ�Ʒÿ��������Ԫ��
��2����Ҫ����A��B���ֽ�Ʒ��100�����ܷ��ò�����900Ԫ����ôA�ֽ�Ʒ������ټ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ǡ�O ��һ�㣬PA�С�O�ڵ�A��AB�ǡ�O��ֱ��������OP������B��BC��OP����O�ڵ�C������AC��OP�ڵ�D��
(1)��֤��PC�ǡ�O�����ߣ�
(2)��PD=cm��AC=8cm����ͼ����Ӱ���ֵ������
(3)��(2)�������£�����E��![]() ���е㣬����CE����CE�ij���
���е㣬����CE����CE�ij���
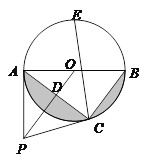
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ŀǰ���ܵ��ڳ����ѻ����ռ���ij�̳��ƻ������ס������ֽ��ܶ���1200ֻ�������ֽ��ܵƵĽ��ۡ��ۼ����±���
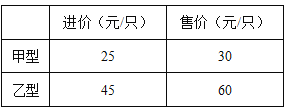
��1����ν�����������ǡ��Ϊ46000Ԫ?
��2��Ϊȷ�����ͽ��ܵ�˳���������ڣ�1���������£��̼Ҿ��������ͽ��ܵƽ��д��۳��ۣ���ȫ����������ͽ��ܵƵ�������Ϊ20%����ͬ���ͽ��ܵ������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�����B��ֱ��l����E��ֱ��l�ϣ�����CE��DE��CE=BC������C��CF��DE�ڵ�F����ֱ��l�ڵ�H����l����ͼ����λ��ʱ����֤��BH+EH=![]() CH������֤������
CH������֤������
��1����l����ͼ����λ��ʱ���߶�BH��EH��CH֮����������������ϵ��д����IJ��룬������֤����
��2����l����ͼ����λ��ʱ���߶�BH��EH��CH֮����������������ϵ��д����IJ��룬����֤����
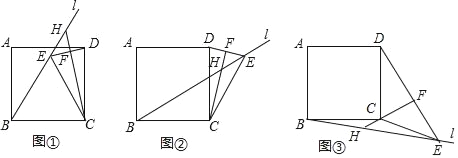
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С����Ҫ�����µ�һ��̽����С������һ�����������������A,B�����ͺŵĸ�������. �������������һ������ˮ����ͼ��ˮ�߶�Ϊ30mm��ˮ������û���еĸ���.̽��һ��С����������ʵ�飬�ȷ���3��A�ͺŸ���ˮ��ĸ߶��ǵ�36mm����3��A�ͺŸ����̳����ٷ���2��B�ͺŸ���ˮ��ĸ߶�ǡ��Ҳ�ǵ�36mm.�ɴ˿�֪A�ͺ���B�ͺŸ���������Ϊ____________��
̽������С����֮ǰ�ĸ���ȫ���̳���Ȼ���ٷ���A�ͺ���B�ͺŸ���10����ˮ��߶��ǵ�57mm���ʷ���ˮ�е�A�ͺ���B�ͺŸ����������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ��һ����������ϵ�ԭ�㿪ʼ���������ƶ�2����λ���ȣ��������ƶ�5����λ���ȣ����Կ����յ��ʾ��-3����֪A��B�������ϵĵ㣬�������ͼ��˼����������и���.
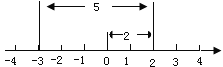
(1)�����A��ʾ����-1������A�����ƶ�4����λ���ȣ���ô�յ�B��ʾ������____.A��B�����ľ�����__________.
(2)�����A��ʾ����2������A�����ƶ�6����λ���ȣ��������ƶ�3����λ���ȣ���ô�յ�B��ʾ������____.A��B�����ľ�����____.
(3)�����A��ʾ����m������A�����ƶ�n����λ���ȣ��������ƶ�p����λ���ȣ���ô��������յ�B��ʾ������___.A��B�����ľ�����______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����C��ֱ�� AB �ϣ� ACa �� BCb ���� ab ���� M���߶� AB ���е㣬���߶� MC�ij�Ϊ�� ��
A.![]() B.
B.![]() C.
C.![]() ��
��![]() D.
D.![]() ��
��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ɽijũ����Ϊ��ץס����һ��С���ٵ��̻�����������A��B���ּ���Ʒ��������A�ּ���Ʒ4����B�ּ���Ʒ3������Ҫ550Ԫ��������A�ּ���Ʒ8����B�ּ���Ʒ5������Ҫ1050Ԫ��
��1����A��B���ּ���Ʒÿ���������Ԫ��
��2������ũ���־������������ּ���Ʒ��100���������г�������ʽ���ת�����ڹ�����100������Ʒ���ʽ�����7500Ԫ����������7650Ԫ����ô��ũ���ֹ��м��ֽ���������
��3��������ÿ��A�ּ���Ʒ�ɻ�����30Ԫ��ÿ��B�ּ���Ʒ�ɻ�����20Ԫ���ڵڣ�2���ʵĸ��ֽ��������У���һ�ַ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com