
【题目】某学校为了美化校园环境,向园林公司购买一批树苗.公司规定:若购买树苗不超过60棵,则每棵树售价120元;若购买树苗超过60棵,则每增加1棵,每棵树售价均降低0.5元,且每棵树苗的售价降到100元后,不管购买多少棵树苗,每棵售价均为100元.
(1)若该学校购买50棵树苗,求这所学校需向园林公司支付的树苗款;
(2)若该学校向园林公司支付树苗款8800元,求这所学校购买了多少棵树苗.
【答案】(1)这所学校需向园林公司支付的树苗款为6000元;(2)这所中学购买了80棵树苗.
【解析】
(1)由题意按照每棵120元进行计算;(2)设设购买了![]() 棵树苗,根据单价×数量=总价列方程,求解.
棵树苗,根据单价×数量=总价列方程,求解.
解:(1)∵![]() ,
,
∴![]() (元),
(元),
∴答:这所学校需向园林公司支付的树苗款为6000元.
(2)∵购买60棵树苗时所需支付的树苗款为![]() 元
元![]() 元,
元,
∴该中学购买的树苗超过60棵.
又∵![]() ,
,
∴购买100棵树苗时每棵树苗的售价恰好降至100元.
∵购买树苗超过100棵后,每棵树苗的售价仍为100元,
此时所需支付的树苗款超过10000元,而![]() ,
,
∴该中学购买的树苗不超过100棵.
设购买了![]() 棵树苗,
棵树苗,
依题意,得![]() ,
,
化简,得![]() ,
,
解得![]() (舍去),
(舍去),![]() .
.
答:这所中学购买了80棵树苗.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图①,△ABC,△CDE都是等边三角形.
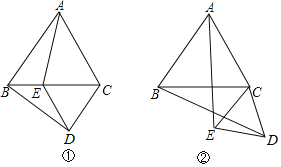
(1)写出AE与BD的大小关系.
(2)若把△CDE绕点C逆时针旋转到图②的位置时,上述(1)的结论仍成立吗?请说明理由.
(3)△ABC的边长为5,△CDE的边长为2,把△CDE绕点C逆时针旋转一周后回到图①位置,求出线段AE长的最大值和最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
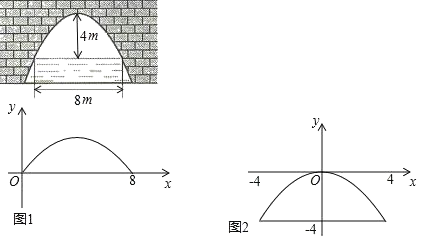
【题目】图中所示的抛物线形拱桥,当拱顶离水面4m时,水面宽8m.水面上升3米,水面宽度减少多少?下面给出了解决这个问题的两种建系方法.
方法一如图1,以上升前的水面所在直线与抛物线左侧交点为原点,以上升前的水面所在直线为x轴,建立平面直角坐标系xOy;
方法二如图2,以抛物线顶点为原点,以抛物线的对称轴为y轴,建立平面直角坐标系xOy,
查看答案和解析>>
科目:初中数学 来源: 题型:
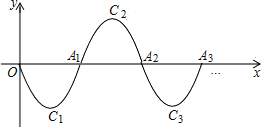
【题目】如图一段抛物线y=x2﹣3x(0≤x≤3),记为C1,它与x轴于点O和A1:将C1绕旋转180°得到C2,交x轴于A2;将C2绕旋转180°得到C3,交x轴于A3,如此进行下去,若点P(2020,m)在某段抛物线上,则m的值为( )
A.0B.﹣![]() C.2D.﹣2
C.2D.﹣2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,若二次函数y=ax2+bx+c(a≠0)图象的对称轴为x=1,与y轴交于点C,与x轴交于点A、点B(﹣1,0),则
①二次函数的最大值为a+b+c;
②a﹣b+c<0;
③b2﹣4ac<0;
④当y>0时,﹣1<x<3,其中正确的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了了解同学们每月零花钱的数额,校园小记者随机调查了本校部分同学,根据调查结果,绘制出了如下两个尚不完整的统计图表.
调查结果统计表
组别 | 分组(单位:元) | 人数 |
A | 0≤x<30 | 4 |
B | 30≤x<60 | 16 |
C | 60≤x<90 | a |
D | 90≤x<120 | b |
E | x≥120 | 2 |
请根据以上图表,解答下列问题:
(1)填空:这次被调查的同学共有__人,a+b=__,m=___;
(2)求扇形统计图中扇形C的圆心角度数;
(3)该校共有学生1000人,请估计每月零花钱的数额x在60≤x<120范围的人数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有4张卡片,4张卡片的正面分别标有数字1、2、3、4,这些卡片除数字外都相同,将卡片搅匀.
(1)从盒子任意抽取一张卡片,恰好抽到标有奇数卡片的概率是 ;
(2)先从盒子中任意抽取一张卡片,再从余下的3张卡片中任意抽取一张卡片,求抽取的2张卡片标有数字之和大于5的概率(请用画树状图或列表等方法求解).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于反比例函数y=﹣![]() ,下列说法错误的是( )
,下列说法错误的是( )
A.图象经过点(1,﹣3)
B.图象分布在第一、三象限
C.图象关于原点对称
D.图象与坐标轴没有交点
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com