
【题目】如图,直线y=kx-3与x轴、y轴分别交于点B,C, ![]() =
= ![]() .
.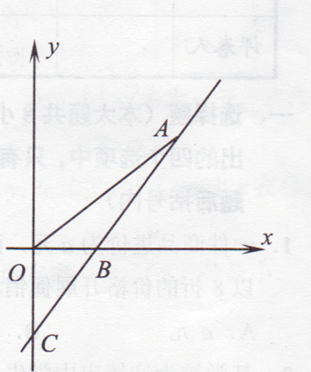
(1)求点B坐标和k值;
(2)若点A(x,y)是直线y=kx-3上在第一象限内的一个动点,当点A在运动过程中,试写出△AOB的面积S与x的函数关系式(不要求写自变量范围);并进一步求出点A的坐标为多少时,△AOB的面积为 ![]() ?
?
(3)在上述条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,请写出满足条件的所有P点坐标;若不存在,请说明理由.
【答案】
(1)
(1)∵直线y=kx-3与y轴的交点为C(0,-3)
∴OC=3
∵ ![]() =
= ![]()
∴OB= ![]()
∴B点坐标为( ![]() ,0)
,0)
将B( ![]() ,0)代入y=kx-3,得
,0)代入y=kx-3,得
![]() k-1=0
k-1=0
解得k=2.
(2)
解:由(1)可知直线的解析式是y=2x-3,
S= ![]() ×OB×yA
×OB×yA
= ![]() ×
× ![]() ×(2x-3)
×(2x-3)
= ![]() x-
x- ![]()
即:三角形AOB的面积S与x的函数关系式为S= ![]() x-
x- ![]() ,
,
当S= ![]() 时,
时, ![]() x-
x- ![]() =
= ![]() ,解得x=3,则2x-3=3,即A(3,3).
,解得x=3,则2x-3=3,即A(3,3).
所以当点A的坐标为(3,3)时,△AOB的面积为 ![]() ?
?
(3)
解:存在.由(2)得A(3,3),AO=3 ![]() ,∠AOB=45°,
,∠AOB=45°,
当OP=AO=3 ![]() 时,P(3
时,P(3 ![]() ,0)或P(-3
,0)或P(-3 ![]() ,0);
,0);
当AP=OA=3 ![]() 时,∠APO=∠AOP=45°,则OP=
时,∠APO=∠AOP=45°,则OP= ![]() OA=6,P(6,0);
OA=6,P(6,0);
当OP=AP时,P(3,0).
【解析】(1)当x=0时,y=-3,即C(0,-3),由 ![]() =
= ![]() 求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S=
求出B点坐标,将它代入直线y=kx-3可求出k;(2)因为点A在直线y=2x-3上,则A(x, 2x-3),由S= ![]() ×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S=
×OB×yA , 代入相应值即可求出S关于x的函数关系式;令S= ![]() 时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3
时,求出x的值,并代入直线解析式求出A点的坐标;(3)分类讨论:当OP=AO时,当AP=OA时,当OP=AP时.结合A(3,3),AO=3 ![]() ,∠AOB=45°解题即可.
,∠AOB=45°解题即可.
【考点精析】本题主要考查了一次函数的性质和一次函数的图象和性质的相关知识点,需要掌握一般地,一次函数y=kx+b有下列性质:(1)当k>0时,y随x的增大而增大(2)当k<0时,y随x的增大而减小;一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远才能正确解答此题.


科目:初中数学 来源: 题型:
【题目】如图 1,是由一些棱长为单位 1 的相同的小正方体组合成的简单几何体.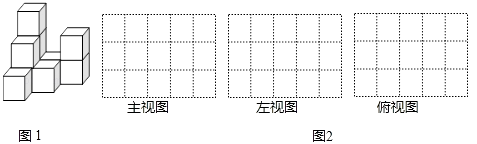
(1)请在图 2 方格纸中分别画出几何体的主视图、左视图和俯视图.
(2)如果在其表面涂漆,则要涂平方单位.(几何体放在地上,底面无法涂上漆)
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把点(2,﹣3)先向右平移3个单位长度,再向下平移2个单位长度得到的点的坐标是( )
A.(5,﹣1)
B.(﹣1,﹣5)
C.(5,﹣5)
D.(﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中最适合普遍调查的是( )
A.调查某品牌灯泡的使用寿命B.调查振兴区居民网上购物情况
C.调查锦江山上各种鸟的总数量D.调查我国大型客机C919的零件质量
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A是双曲线y= ![]() 在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( )
在第一象限上的一动点,连接AO并延长交另一分支于点B,以AB为斜边作等腰Rt△ABC,点C在第二象限,随着点A的运动,点C的位置也不断的变化,但始终在一函数图象上运动,则这个函数的解析式为( ) 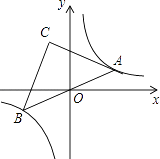
A.y= ![]()
B.y= ![]()
C.y=﹣ ![]()
D.y=﹣ ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县2011年初中毕业生的实验考查成绩等级的分布情况,随机抽取了该县若干名学生的实验考查成绩进行统计分析,并根据抽取的成绩绘制了如下的统计图表:
成绩等级 | A | B | C | D |
人数 | 60 | x | y | 10 |
百分比 | 30% | 50% | 15% | m |
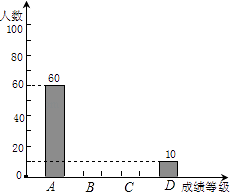
请根据以上统计图表提供的信息,解答下列问题:
(1)本次抽查的学生有名;
(2)表中x,y和m所表示的数分别为:x= , y= , m=;
(3)请补全条形统计图;
(4)根据抽样调查结果,请你估计2011年该县5400名初中毕业生实验考查成绩为D类的学生人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com