
【题目】下列说法:①函数![]() 的自变量
的自变量![]() 的取值范围是
的取值范围是![]() ;②对角线相等的四边形是矩形;③正六边形的中心角为
;②对角线相等的四边形是矩形;③正六边形的中心角为![]() ;④对角线互相平分且相等的四边形是菱形;⑤计算
;④对角线互相平分且相等的四边形是菱形;⑤计算![]() 的结果为7:⑥相等的圆心角所对的弧相等;⑦
的结果为7:⑥相等的圆心角所对的弧相等;⑦![]() 的运算结果是无理数.其中正确的个数有( )
的运算结果是无理数.其中正确的个数有( )
A.1个B.2个C.3个D.4个
科目:初中数学 来源: 题型:
【题目】某中学对本校初2017届500名学生中中考参加体育加试测试情况进行调查,根据男生1000米及女生800米测试成绩整理,绘制成不完整的统计图,(图①,图②),请根据统计图提供的信息,回答下列问题:
(1)该校毕业生中男生有 人;扇形统计图中a= ;
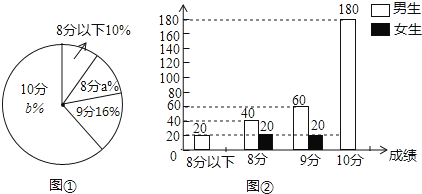
(2)补全条形统计图;
(3)若500名学生中随机抽取一名学生,这名学生该项成绩在8分及8分以下的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展“我最喜爱的一项体育活动”调查,要求每名学生必选且只能选一项.现随机抽查了部分学生,并将其结果绘制成如下不完整的条形图和扇形图.
抽取的学生最喜欢体育活动的条形统计图
抽取的学生最喜欢体育活动的扇形统计图
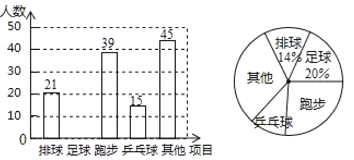
请结合以上信息解答下列问题:
(1)在这次调查中一共抽查了_____学生,扇形统计图中“乒乓球”所对应的圆心角为_____度,并请补全条形统计图;
(2)己知该校共有1200名学生,请你估计该校最喜爱跑步的学生人数;
(3)若在“排球、足球、跑步、乒乓球”四个活动项目任选两项设立课外兴趣小组,请用列表法或画树状图的方法求恰好选中“排球、乒乓球”这两项活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级获得一个到高校体验的名额,从前期的选拔中,小明和小刚从众多报名者中脱颖而出:为公平起见,学校设计了如下的游戏:四张大小、质地相同的卡片上分别标有数字1、2、3、4.将标有数字的一面朝下,洗匀后从中抽取一张卡片,记下上面的数字,不放画,再从剩余的卡片中抽取一张卡片,记下上面的数字如果两次抽取卡片上数字之和是奇数,小明获胜:如果两次抽取卡片上数字之和是偶数,小刚获胜,获胜的同学将代表学校参加“高校体验”活动.请问:学校设计的这个游戏是否公平?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文化源远流长,文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”某中学为了解学生对四大名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如下尚不完整的统计图.
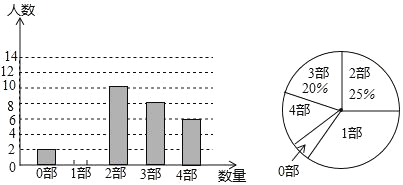
请根据以上信息,解决下列问题
(1)本次调查所得数据的众数是____部,中位数是_____部;
(2)扇形统计图中“4部”所在扇形的圆心角为_____度;
(3)请将条形统计图补充完整;
(4)没有读过四大古典名著的两名学生准备从中各自随机选择一部来阅读,求他们恰好选中同一名著的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、 下旬)日人均阅读时间的情况:
(1)从统计图可知,九年级(1)班共有学生多少人;
(2)求图22.1中a的值;
(3)从图22-1、22-2 中判断,在这次读书月活动中,该班学生每日阅读时间_______(填“普遍增加了”或“普遍减少了”);
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1(即0.5≤t<10)小 时的人数比活动开展初期增加了多少人.
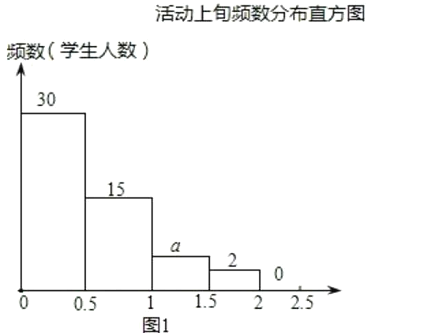


(每个小矩形含左端点,不含右端点) .
查看答案和解析>>
科目:初中数学 来源: 题型:
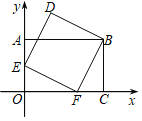
【题目】如图,在平面直角坐标系xOy中,点A、C、F在坐标轴上,E是OA的中点,四边形AOCB是矩形,四边形BDEF是正方形,若点C的坐标为(3,0),则点D的坐标为( )
A. (1,2.5)B. (1,1+ ![]() )C. (1,3)D. (
)C. (1,3)D. (![]() ﹣1,1+
﹣1,1+ ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
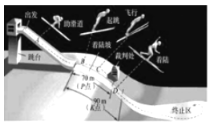
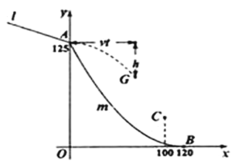
【题目】跳台滑雪是冬季奥运会比赛项目之一,如图平面直角坐标系是跳台滑雪的截面示意图,运动员沿滑道![]() 下滑,在
下滑,在![]() 轴上的点
轴上的点![]() 起跳,点
起跳,点![]() 距落地水平面
距落地水平面![]() 轴
轴![]() ,运动员落地的雪面开始是一段曲线
,运动员落地的雪面开始是一段曲线![]() ,到达点
,到达点![]() 后变为水平面,点
后变为水平面,点![]() 距
距![]() 轴的水平距离为
轴的水平距离为![]() .运动员(看成点)从点
.运动员(看成点)从点![]() 起跳后的水平速度为
起跳后的水平速度为![]() ,点
,点![]() 是下落路线的某位置.忽略空气阻力,实验表明:
是下落路线的某位置.忽略空气阻力,实验表明:![]() ,
,![]() 的竖直距离
的竖直距离![]() 与飞出时间
与飞出时间![]() 的平方成正比,且
的平方成正比,且![]() 时
时![]() ;
;![]() ,
,![]() 的水平距离是
的水平距离是![]() 米.
米.
(1)用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)用含![]() 、
、![]() 的代数式表示点
的代数式表示点![]() 的横坐标
的横坐标![]() 和纵坐标
和纵坐标![]() ,并求
,并求![]() 与
与![]() 的关系式(不写
的关系式(不写![]() 的取值范围);
的取值范围);
(3)奥运组委会规定,运动员落地点距起跳点的水平距离为运动员本次跳跃的成绩,并且参赛的达标成绩为![]() .在运动员跳跃的过程中,点
.在运动员跳跃的过程中,点![]() 处有一个摄像头,记录运动员的空中姿态,当运动员飞过点
处有一个摄像头,记录运动员的空中姿态,当运动员飞过点![]() 时,在点
时,在点![]() 上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被
上方可被摄像头抓拍到.若运动员本次跳跃达到达标成绩,并且能被![]() 处摄像头抓拍,求从点
处摄像头抓拍,求从点![]() 起跳后的水平速度
起跳后的水平速度![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
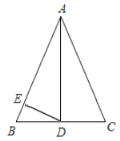
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是边
是边![]() 的中点,过点
的中点,过点![]() 作
作![]() 于点
于点![]() ,
,![]() 的外接圆与边
的外接圆与边![]() 交于点
交于点![]() ,
,![]() ,
,
(1)①补全图形;②判断直线![]() 与
与![]() 的外接圆的公共点个数,并给出证明.
的外接圆的公共点个数,并给出证明.
(2)若![]() ,
,![]() ,求线段
,求线段![]() 的长度.
的长度.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com