Question

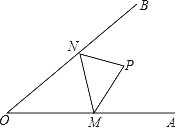
【题目】如图，点P是∠AOB内任意一点，且∠AOB=40°，点M和点N分别是射线OA和射线OB上的动点，当△PMN周长取最小值时，则∠MPN的度数为_____．

Answer 1

【答案】100°

【解析】

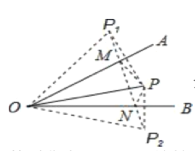
分别作点P关于OA、OB的对称点P 、P ，连P 、P，交OA于M，交OB于N，△PMN的周长= PP，然后得到等腰△OP1P2中，∠O PP+∠O PP=100°，即可得出∠MPN=∠OPM+∠OPN=∠OPM+∠OPN=100°．

分别作点P关于OA、OB的对称点P 、P,连接PP，交OA于M，交OB于N，则

O P=OP=OP,∠OPM=∠MPO,∠NPO=∠NPO，

根据轴对称的性质,可得MP=PM,PN=PN，则

△PMN的周长的最小值=PP，

∴∠POP=2∠AOB=80°，

∴等腰△OPP中,∠OPP+∠OPP=100°，

∴∠MPN=∠OPM+∠OPN=∠OPM+∠OPN=100°，

故答案为100°