
����Ŀ��2019��4��25����27�գ��ڶ�����һ��һ·�����ʺ����߷���̳�ڱ������У�������̳�ڼ䣬�й�ͬ30�������ǩ��ó����Э�顣�ҹ�����![]() �صIJ�Ҷ1000�ֺ�
�صIJ�Ҷ1000�ֺ�![]() �صIJ�Ҷ500��������һ��һ·�����ߵ�
�صIJ�Ҷ500��������һ��һ·�����ߵ�![]() �غ�
�غ�![]() �أ�
�أ�![]() �غ�
�غ�![]() �ضԲ�Ҷ����ֱ�Ϊ900�ֺ�600�֣���֪��
�ضԲ�Ҷ����ֱ�Ϊ900�ֺ�600�֣���֪��![]() ��
��![]() �����˲�Ҷ��
�����˲�Ҷ��![]() ��
��![]() ���ص��˷ѣ�Ԫ/�֣����±���ʾ����
���ص��˷ѣ�Ԫ/�֣����±���ʾ����![]() ���˵�
���˵�![]() �صIJ�ҶΪ
�صIJ�ҶΪ![]() �֣�
�֣�
|
| |
| 35 | 40 |
| 30 | 45 |
��1���ú�![]() �Ĵ���ʽ��գ�
�Ĵ���ʽ��գ�![]() ������
������![]() �صIJ�Ҷ����Ϊ___________��
�صIJ�Ҷ����Ϊ___________��![]() ������
������![]() �صIJ�Ҷ����Ϊ___________��
�صIJ�Ҷ����Ϊ___________��![]() ������
������![]() �صIJ�Ҷ����Ϊ___________.
�صIJ�Ҷ����Ϊ___________.
��2���ú�![]() ���֣��Ĵ���ʽ��ʾ���˷�
���֣��Ĵ���ʽ��ʾ���˷�![]() ��Ԫ������ֱ��д���Ա���
��Ԫ������ֱ��д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3����������˷ѣ���˵�����˷����ʱ�����ͷ���.
���𰸡���1��![]() ��
��![]() ��
��![]() ����2��
����2��![]() ����3����
����3����![]() ������
������![]() ��400�֣�����
��400�֣�����![]() ��600�֣���
��600�֣���![]() ������
������![]() ��500��ʱ�˷����
��500��ʱ�˷����
��������
��1����A������C��x�֣�A����1000�֣�����ֻ������D�أ�1000-x���֣�C����Ҫ900�֣���ôB������C�أ�900-x����D����Ҫ600�֣���ô����D��x-400���֣�
��2���������˷�=A������C���˷�+A������D���˷�+B������C���˷�+B������D���˷Ѵ�����ֵ����ĸ�ɵã�
��3�����ݣ�2���еõ���һ�κ�����ϵʽ����Ϻ��������ʺ�ȡֵ��Χȷ�����˷���ͷ�����
��1��![]() ��
��![]() ��
��![]()
��2��![]()
![]() ��
��![]() ��
��
��3����![]() ��
��
��![]() ��
��![]() �����������
�����������
��![]()
�൱![]() ʱ��
ʱ��![]() ��С
��С![]() .
.
����![]() ������
������![]() ��400�֣�����
��400�֣�����![]() ��600�֣�
��600�֣�
��![]() ������
������![]() ��500��ʱ�˷���͡�
��500��ʱ�˷���͡�


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ���ı���ABCD�У�EΪAD���е㣬��֪��DEF�����ΪS�����ı���ABCE�����Ϊ��������
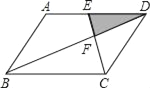
A. 8S B. 9S C. 10S D. 11S
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪������A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB��|a��b|������ʽ��|x��3|�ļ��������������ϱ�ʾ������3�ĵ����ʾ������x�ĵ�֮��ľ��룮
�����������ϣ�ֱ����������𰸣�
��1��|5������2��|��ֵΪ_____��
��2����|x��3|��1����x��ֵΪ_____��
��3����|x��3|��|x+1|����x��ֵΪ_____��
��4����|x��3|+|x+1|��7����x��ֵΪ_____��
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
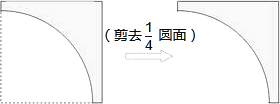
����Ŀ�����ڰ�һ��������ֽƬ����ͼ��ʽ��ȥһ���뾶Ϊ40![]() ����Բ���õ���ͼֽƬ���Ҹ�ֽƬ���ܼ��������Բ��ֽƬ�պ�����ǰ������������ֽƬΧ��һԲ���棬���������ֽƬ�ı߳�ԼΪ�����������ף���������ġ��ص��������ȷ��1���ף�
����Բ���õ���ͼֽƬ���Ҹ�ֽƬ���ܼ��������Բ��ֽƬ�պ�����ǰ������������ֽƬΧ��һԲ���棬���������ֽƬ�ı߳�ԼΪ�����������ף���������ġ��ص��������ȷ��1���ף�![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��
A. 64 B. 67 C. 70 D. 73
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���߳�Ϊ4��������ABCD��������O���е�ֱ�ΪE��F��G��H����ͼ����Ӱ���ֵ����Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ֱ��l��������������m��q��n����m��q������ֱ�Ϊ5��11����n�������������
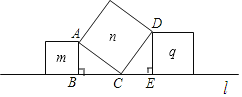
A.4B.6C.16D.55
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ƶ��������Ŀ��ٷ�չ�����ڻ������Ĺ�������Ӧ�˶�����Ϊ�˽�ijС������ʹ�ù��������������ij�о�С������ɷø�С����10λ���õ���10λ����һ����ʹ�ù��������Ĵ����ֱ�Ϊ��17��12��15��20��17��0��7��26��17��9��
��1���������ݵ���λ������ ������������ ����
��2��������10λ����һ����ʹ�ù���������ƽ��������
��3������С����200�������Թ��Ƹ�С������һ����ʹ�ù����������ܴ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ�����ı���ABCD�У���A=��C=90�㣬BEƽ�֡�ABC��DFƽ�֡�ADC��BE��DF��������λ�ù�ϵ��Ϊʲô��
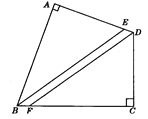
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com