
【题目】某仓库为了保持库内的湿度和温度,四周墙上均装有如图所示的自动通风设施.该设施的下部ABCD是矩形,其中AB=2米,BC=1米;上部△CDG是等边三角形,固定点E为AB的中点.△EMN是由电脑控制其形状变化的三角通风窗(阴影部分均不通风),MN是可以沿设施边框上下滑动且始终保持和AB平行的伸缩横杆.
(1)当MN和AB之间的距离为0.5米时,求此时△EMN的面积;
(2)设MN与AB之间的距离为x 米,试将△EMN的面积S(平方米)表示成关于x的函数;
(3)请你探究△EMN的面积S(平方米)有无最大值,若有,请求出这个最大值;若没有,请说明理由.

【答案】(1)0.5平方米;(2)0<x≤1时,S=x;1<x<![]() 时,S=
时,S= ![]() ;(3)1或
;(3)1或![]()
【解析】试题分析:(1)要看图解答问题.得出当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN边上的高为0.5米可得出三角形EMN的面积;
(2)本题要分情况解答(0<x≤1;1<x<1+![]() ).当0<x≤1时,可直接得出三角形的面积函数;当1<x<1+
).当0<x≤1时,可直接得出三角形的面积函数;当1<x<1+![]() ,连接EG,交CD于点F,交MN于点H,先求FG,再证△MNG∽△DCG,继而得出三角形面积函数;
,连接EG,交CD于点F,交MN于点H,先求FG,再证△MNG∽△DCG,继而得出三角形面积函数;
(3)本题也要分两种情况解答:当MN在矩形区域滑动时以及当MN在三角形区域滑动时),利用二次函数的性质解答.当MN在矩形区域滑动时,S=x,可直接由图得出取值范围;当MN在三角形区域滑动时,由二次函数性质可知,在对称轴时取得最大值.
试题解析:(1)由题意,当MN和AB之间的距离为0.5米时,MN应位于DC下方,且此时△EMN中MN=AB=2米,MN边上的高为0.5米.
所以,S△EMN=![]() =0.5(平方米).
=0.5(平方米).
即△EMN的面积为0.5平方米.
(2)①当MN在矩形区域滑动时,即0<x≤1时,此时MN=AB=2米,
∴△EMN的面积S= ![]() ;
;
②当MN在三角形区域滑动,即1<x<![]() 时.如图,连接EG,交CD于点F,交MN于点H,
时.如图,连接EG,交CD于点F,交MN于点H,

∵ E为AB中点,
∴易得 F为CD中点,
GF⊥CD,且FG=![]() .
.
∴GH= ![]() ,
,
又∵ MN∥CD,
∴ △MNG∽△DCG.
∴![]() ,
,
∴![]() ,即
,即![]() .
.
故△EMN的面积S=![]() =
=![]() =
=![]() ;
;
(3)①当MN在矩形区域滑动时,
S= ![]() ,
, ![]() ,所以当
,所以当![]() =1时,有S最大= 1;
=1时,有S最大= 1;
②当MN在三角形区域滑动时,
S= ![]() ,(1<x<
,(1<x<![]() ).
).
所以,当![]() =
=![]() 时,有S最大=
时,有S最大= ![]()
综合①、②得:当![]() =
=![]() 时,S的最大值为
时,S的最大值为![]() 平方米.
平方米.


科目:初中数学 来源: 题型:
【题目】已知某校田径队25人年龄的平均数和中位数都是16岁,但是后来发现其中有一位同学的年龄登记错误,将17岁写成了19岁,经重新计算后,正确的平均数为a岁,中位数为b岁,则下列结论中正确的是( )
A. a>16,b=16 B. a>16,b<16 C. a<16,b<16 D. a<16,b=16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】心理学家研究发现,一般情况下,学生的注意力随着老师讲课时间的变化而变化,讲课开始时,学生的注意力逐步增强,中间有一段时间学生的注意力保持较为理想的状态,随后学生的注意力开始分散.经过实验分析可知,学生的注意力y随时间t(分钟)的变化规律有如下关系式:  (y值越大表示接受能力越强)
(y值越大表示接受能力越强)
(1)讲课开始后第5分钟时与讲课开始后第25分钟时比较,何时学生的注意力更集中;
(2)讲课开始后多少分钟,学生的注意力最集中能持续多少分钟;
(3)一道数学难题,需要讲解24分钟,为了效果较好,要求学生的注意力最低达到180,那么经过适当安排,老师能否在学生注意力达到所需的状态下讲解完这道题目?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l是四边形ABCD的对称轴.若AD∥BC,则下列结论:(1)AB∥CD;(2)AB=BC;(3)BD平分∠ABC;(4)AO=CO.其中正确的有______(填序号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,动点P从点A开始沿A→B→C→D 的路径匀速前进到D为止.在这个过程中,△APD的面积S随时间t的变化关系用图象表示正确的是( )

A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:初中数学 来源: 题型:
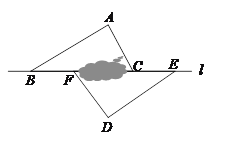
【题目】如图,点B、F、C、E在直线l上(F、C之间不能直接测量),点A、D在l异侧,测得AB=DE,AB∥DE,∠A=∠D.
(1)求证:△ABC≌△DEF;
(2)若BE=10m,BF=3m,求FC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D是BC边的中点,点E,F分别在AC,AB上,且DE∥AB,EF∥BC.
(1)求证:CD=EF;
(2)已知∠ABC=60°,连接BE,若BE平分∠ABC,CD=6,求四边形BDEF的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的图像交y轴于C点,交
的图像交y轴于C点,交![]() 轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程
轴于A,B两点(点A在点B的左侧),点A、点B的横坐标是一元二次方程![]() 的两个根.
的两个根.
(1)求出点A、点B的坐标及该二次函数表达式.

(2)如图2,连接AC、BC,点Q是线段OB上一个动点(点Q不与点O、B重合),过点Q作QD∥AC交于BC点D,设Q点坐标(m,0),当△CDQ面积S最大时,求m的值.
(3)如图3,线段MN是直线y=x上的动线段(点M在点N左侧),且MN=![]() ,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
,若M点的横坐标为n,过点M作x轴的垂线与x轴交于点P,过点N作x轴的垂线与抛物线交于点Q.以点P,M,Q,N为顶点的四边形能否为平行四边形?若能,请求出n的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com