
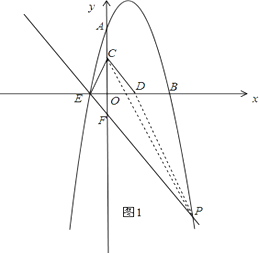
����Ŀ����ͼ����֪������y=�� ![]() x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
��1��ֱ��д�������ߵĽ���ʽ����
��2�����CED�����S��D���˶�ʱ��t�ĺ�������ʽ����tΪ��ֵʱ����CED���������������Ƕ��٣�
��3������CED��������ʱ�������������Ƿ���ڵ�P����E���⣩��ʹ��PCD��������ڡ�CED���������������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��y=�� ![]() x2+3x+8
x2+3x+8
��2��
�⣺�ߵ�A��0��8����B��8��0����
��OA=8��OB=8��
��y=0����� ![]() x2+3x+8=0��
x2+3x+8=0��
��ã�x1=8��x2=��2��
�ߵ�E��x��ĸ������ϣ�
���E����2��0����
��OE=2��
��������ã���D���˶�t��ʱ��BD=t��OC=t��
��OD=8��t��
��DE=OE+OD=10��t��
��S= ![]() DEOC=
DEOC= ![]() ��10��t��t=��
��10��t��t=�� ![]() t2+5t��
t2+5t��
��S=�� ![]() t2+5t=��
t2+5t=�� ![]() ��t��5��2+
��t��5��2+ ![]() ��
��
�൱t=5ʱ��S���= ![]()
��3��
�⣺����һ��
�ɣ�2��֪����t=5ʱ��S���= ![]() ��
��
�൱t=5ʱ��OC=5��OD=3��
��C��0��5����D��3��0����
�ɹ��ɶ����ã�CD= ![]() ��
��
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
��C��0��5����D��3��0����������ʽ�ã�
k=�� ![]() ��b=5��
��b=5��
��ֱ��CD�Ľ���ʽΪ��y=�� ![]() x+5��
x+5��
��E����EF��CD�������������P����ͼ1��
��ֱ��EF�Ľ���ʽΪ��y=�� ![]() x+b��
x+b��
��E����2��0������ã�b=�� ![]() ��
��
��ֱ��EF�Ľ���ʽΪ��y=�� ![]() x��
x�� ![]() ��
��
��y=�� ![]() x��
x�� ![]() ����y=��
����y=�� ![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
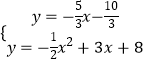 ��
��
��ã� ![]() ��
�� 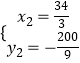 ��
��
��P�� ![]() ����
���� ![]() ����
����
����E��EG��CD������ΪG��
�ߵ�t=5ʱ��S��ECD= ![]() =
= ![]() ��
��
��EG= ![]() ��
��
����D��DN��CD������ΪN����ʹDN= ![]() ������N��NM��x�ᣬ����ΪM����ͼ2��
������N��NM��x�ᣬ����ΪM����ͼ2��
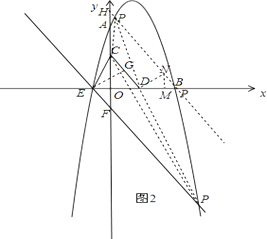
�ɵá�EGD�ס�DMN��
�� ![]() ��
��
����  ��
��
��ã�DM= ![]() ��
��
��OM= ![]() ��
��
�ɹ��ɶ����ã�MN= ![]() =
= ![]() ��
��
��N�� ![]() ��
�� ![]() ����
����
����N��NH��CD���������߽����P����ͼ2��
��ֱ��NH�Ľ���ʽΪ��y=�� ![]() x+b��
x+b��
��N�� ![]() ��
�� ![]() ����������ʽ�ã�b=
����������ʽ�ã�b= ![]() ��
��
��ֱ��NH�Ľ���ʽΪ��y=�� ![]() x+
x+ ![]() ��
��
��y=�� ![]() x+
x+ ![]() ����y=��
����y=�� ![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
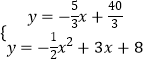 ��
��
��ã� ![]() ��
�� 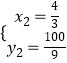 ��
��
��P��8��0����P�� ![]() ��
�� ![]() ����
����
��������������CED��������ʱ�����������ϴ��ڵ�P����E���⣩��ʹ��PCD��������ڡ�CED������������P������Ϊ��P�� ![]() ����
���� ![]() ����P��8��0����P��
����P��8��0����P�� ![]() ��
�� ![]() ����
����
��������
�ɣ�2��֪��C��0��5����D��3��0������lCD��y=�� ![]() x+5��
x+5��
��PH��x�ᣬ��CD�ڵ�H��
��P���������ϣ�����P��6m����18m2+18m+8����
��H��6m����10m+5����C��0��5����D��3��0����
S��PCD= ![]() |��DX��CX����PY��HY��|��
|��DX��CX����PY��HY��|��
��S��CED= ![]() ��
��
�� ![]() ��
��
��3��|18m2��28m��3|=25��
��3����18m2��28m��3��=25��
��m1=�� ![]() ��m2=
��m2= ![]() ��
��
��6m1=��2���ᣩ��6m2= ![]() ��
��
��3����18m2��28m��3��=��25��
��m1= ![]() ��m2=
��m2= ![]() ��
��
��6m1=8��6m2= ![]() ��
��
������������P��������P�� ![]() ����
���� ![]() ����P��8��0����P��
����P��8��0����P�� ![]() ��
�� ![]() ��
��
���������⣺��1������A��0��8����B��8��0������������y=�� ![]() x2+bx+c�ã�
x2+bx+c�ã� 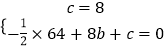 ��
��
��ã�b=3��c=8��
�������ߵĽ���ʽΪ��y=�� ![]() x2+3x+8��
x2+3x+8��
���Դ��ǣ�y=�� ![]() x2+3x+8��
x2+3x+8��
�����㾫����������Ҫ�����˶��κ�����ͼ��Ͷ��κ��������ʵ����֪ʶ�㣬��Ҫ���ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��������y=��x2+bx+c��x�ύ��A��2��0����B����4��0�����㣮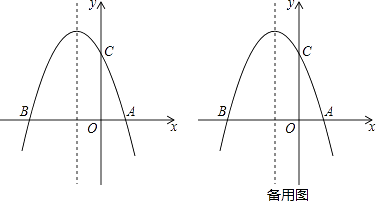
��1����������ߵĽ���ʽ��
��2���������߽�y����C�㣬�ڸ������ߵĶԳ������Ƿ���ڵ�Q��ʹ�á�QAC���ܳ���С�������ڣ����Q������ꣻ�������ڣ���˵�����ɣ�
��3���������ߵĵڶ�����ͼ�����Ƿ����һ��P��ʹ�á�PBC�������������ڣ������P�����꼰��PBC��������ֵ�������棬��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����ı���ABCD�У�AB=BC���Խ���BDƽ��ABC��P��BD��һ�㣬����P��PM^AD��PN^CD������ֱ�ΪM��N��
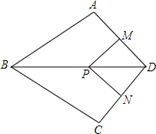
��1����֤��ADB=CDB��
��2����ADC=90������֤���ı���MPND�������Ρ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬ��ABC��AB��8��BC��6��AC��5���ع���B��ֱ���۵���������Σ��ۺ�ΪBD����D���߶�AC���Ҳ���A��C�غϣ�������C����AB���·��ĵ�E�������ADE���ܳ�p��ȡֵ��Χ�ǣ� ��

A. 7��p��10 B. 5��p��10 C. 5��p��7 D. 7��p��19
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ڡ�ABC�У���CAB��2������0�㣼����30�㣬APƽ�֡�CAB��
��1����ͼ��������21�㣬��ABC��32������AP��BC�ڵ�P����̽���߶�AB��AC��PB֮���������ϵ��������Ľ��ۼ���֤����

��2����ͼ������ABC��60�㣭������P�ڡ�ABC���ڲ�����ʹ��CBP��30����ֱ��д����APC�Ķ���________���ú����Ĵ���ʽ��ʾ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
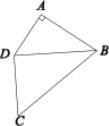
����Ŀ����ͼ��ʾ�����ı���ABCD������AΪֱ����AB��16��BC��25��CD��15��AD��12��
(1)��˵��BD��CD
(2)���ı���ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���AOBC�У���A�������ǣ���2��1������C����������4����B��C���������ֱ��ǣ� �� 
A.�� ![]() ��3��������
��3�������� ![]() ��4��
��4��
B.�� ![]() ��3��������
��3�������� ![]() ��4��??
��4��??
C.�� ![]() ��
�� ![]() ��������
�������� ![]() ��4��
��4��
D.�� ![]() ��
�� ![]() ��������
�������� ![]() ��4��
��4��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com