
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌШєЕуPЕФзјБъЮЊ![]() ,дђЖЈвхЃК
,дђЖЈвхЃК ![]() ЮЊЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБ.
ЮЊЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБ.
ЃЈ1ЃЉШєвбжЊPЃЈ-2ЃЌ3ЃЉЃЌдђЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈ-2ЃЌ3ЃЉ= ЃЛ
ЃЈ2ЃЉШєЕуPЃЈxЃЌyЃЉТњзу2x+y=0,ЧвЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈxЃЌyЃЉ=6ЃЌЧѓГіPЕФзјБъЃЛ
ЃЈ3ЃЉШєЕуPЕНзјБъдЕуOЕФЁАелЯпОрРыЁБdЃЈxЃЌyЃЉ=3ЃЌЪддкзјБъЯЕФкЛГіЫљгаТњзуЬѕМўЕФЕуPЙЙГЩЕФЭМаЮЃЌВЂЧѓГіИУЭМаЮЕФЫљЮЇГЩЗтБеЧјгђЕФУцЛ§.

ЁОД№АИЁПЃЈ1ЃЉ5ЃЛЃЈ2ЃЉЃЈ2ЃЌ-4ЃЉЃЌЃЈ-2,4ЃЉЃЌЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛЃЈ3ЃЉЛЭММћНтЮіЃЌУцЛ§ЮЊ18.
ЁОНтЮіЁПЪдЬтЗжЮіЃКЃЈ1ЃЉИљОнЖЈвхЧѓГіМДПЩЃЛЃЈ2ЃЉгЩdЃЈxЃЌyЃЉ=![]() =6ЃЌдйгЩ2x+y=0СНЪНЧѓГіxЁЂyЃЛЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=
=6ЃЌдйгЩ2x+y=0СНЪНЧѓГіxЁЂyЃЛЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=![]() =3ЃЌЕУГіЂйy=-x+3ЃЛЂкy=x-3ЃЛЂлy=x+3ЃЛЂмy=-x-3.ЗжБ№ЛГіЫФЬѕжБЯпЃЌдйЧѓЮЇГЩУцЛ§.
=3ЃЌЕУГіЂйy=-x+3ЃЛЂкy=x-3ЃЛЂлy=x+3ЃЛЂмy=-x-3.ЗжБ№ЛГіЫФЬѕжБЯпЃЌдйЧѓЮЇГЩУцЛ§.
НтЃКЃЈ1ЃЉdЃЈ-2ЃЌ3ЃЉ=![]() =5ЃЛ
=5ЃЛ
ЃЈ2ЃЉгЩdЃЈxЃЌyЃЉ=![]() =6ЃЌгж2x+y=0ЃЌдђЂй
=6ЃЌгж2x+y=0ЃЌдђЂй![]() НтЕУ
НтЕУ![]() Ђк
Ђк![]() НтЕУ
НтЕУ![]() Ђл
Ђл![]() НтЕУ
НтЕУ![]() Ђм
Ђм![]() НтЕУ
НтЕУ![]() дђЕуPзјБъЮЊЃЈ2ЃЌ-4ЃЉЁЂЃЈ-2,4ЃЉЁЂЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛ
дђЕуPзјБъЮЊЃЈ2ЃЌ-4ЃЉЁЂЃЈ-2,4ЃЉЁЂЃЈ6ЃЌ-12ЃЉЛђЃЈ-6,12ЃЉЃЛ
ЃЈ3ЃЉгЩdЃЈxЃЌyЃЉ=![]() =3ЃЌдђЂйx+y=3,ЕУy=-x+3ЃЛЂкx-y=3ЃЌЕУy=x-3ЃЛЂл-x+y=3ЃЌЕУy=x+3ЃЛЂм-x-y=3ЃЌЕУy=-x-3.
=3ЃЌдђЂйx+y=3,ЕУy=-x+3ЃЛЂкx-y=3ЃЌЕУy=x-3ЃЛЂл-x+y=3ЃЌЕУy=x+3ЃЛЂм-x-y=3ЃЌЕУy=-x-3.
ЛГіЭМЯѓЮЊ
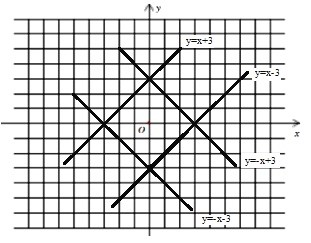
ЮЇГЩЧјгђУцЛ§ЮЊ4ЁС![]() ЁС3ЁС3=18.
ЁС3ЁС3=18.


 бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ
бЇЖјгХЪюЦкЯЮНгФЯОЉДѓбЇГіАцЩчЯЕСаД№АИ Happy holidayЛЖРжМйЦкЪюМйзївЕЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
Happy holidayЛЖРжМйЦкЪюМйзївЕЙуЖЋШЫУёГіАцЩчЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌDЮЊBCБпЕФжаЕуЃЌЙ§DЕуЗжБ№зїDEЁЮABНЛACгкЕуEЃЌDFЁЮACНЛABгкЕуFЃЎ
ЧѓжЄЃКBF=DEЃЎ

ЁОД№АИЁПжЄУїМћНтЮі
ЁОНтЮіЁПЪдЬтЗжЮіЃКИљОнСНзщЖдБпЗжБ№ЦНааЕФЫФБпаЮЮЊЦНааЫФБпаЮПЩХаЖЈЫФБпаЮAFDEЪЧЦНааЫФБпаЮЃЌИљОнЦНааЫФБпаЮЕФаджЪПЩЕУDE=AFЃЌдйгЩDЮЊBCБпЕФжаЕуЃЌDFЁЮACЃЌПЩЕУBF=AFЃЌМДПЩЕУBF=DEЃЎ
ЪдЬтНтЮіЃК
ЁпDEЁЮABЃЌDFЁЮACЃЌ
ЁрDEЁЮAFЃЌDFЁЮAEЃЌ
ЁрЫФБпаЮAFDEЪЧЦНааЫФБпаЮЃЌ
ЁрDE=AFЃЌ
ЁпDЮЊBCБпЕФжаЕуЃЌ
ЁрBD=DCЃЌЁпDFЁЮACЃЌ
ЁрBF=AFЃЌ
ЁрBF=DEЃЎ
ЁОЬтаЭЁПНтД№Ьт
ЁОНсЪјЁП
26
ЁОЬтФПЁПШчЭМЃЌвбжЊЃКЁЯC=ЁЯDЃЌOD=OCЃЎЧѓжЄЃКDE=CEЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкжБНЧзјБъЯЕжаЃЌЮвУЧАбКсЁЂзнзјБъЖМЮЊећЪ§ЕФЕуГЦЮЊећЕуЃЌМЧЖЅЕуЖМЪЧећЕуЕФШ§НЧаЮЮЊећЕуШ§НЧаЮЃЎШчЭМЃЌвбжЊећЕуAЃЈ2ЃЌ3ЃЉЃЌBЃЈ4ЃЌ4ЃЉЃЌЧыдкЫљИјЭјИёЧјгђЃЈКЌБпНчЃЉЩЯАДвЊЧѓЛећЕуШ§НЧаЮЃЎ
ЃЈ1ЃЉдкЭМ1жаЛвЛИіЁїPABЃЌЪЙЕуPЕФКсЁЂзнзјБъжЎКЭЕШгкЕуAЕФКсзјБъЃЛ
ЃЈ2ЃЉдкЭМ2жаЛвЛИіЁїPABЃЌЪЙЕуPЃЌBКсзјБъЕФЦНЗНКЭЕШгкЫќУЧзнзјБъКЭЕФ4БЖЃЎ


ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=x2+bx+cОЙ§AЃЈЉ1ЃЌ0ЃЉЁЂBЃЈ3ЃЌ0ЃЉСНЕуЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНКЭЖЅЕузјБъЃЛ
ЃЈ2ЃЉЕБ0ЃМxЃМ3ЪБЃЌЧѓyЕФШЁжЕЗЖЮЇЃЛ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТСаЫЕЗЈе§ШЗЕФЪЧЃЈ ЃЉ
A. Й§вЛЕугаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпЦНаа.
B. дкЭЌвЛЦНУцФкЃЌЙ§вЛЕугаЧвжЛгавЛЬѕжБЯпгывбжЊжБЯпДЙжБ.
C. гаЙЋЙВЖЅЕуЧвгавЛЬѕЙЋЙВБпЕФСНИіНЧЛЅЮЊСкВЙНЧ.
D. ЯрЕШЕФСНИіНЧЪЧЖдЖЅНЧ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЙћЙигкxЕФвЛдЊЖўДЮЗНГЬax2+bx+c=0гаСНИіЪЕЪ§ИљЃЌЧвЦфжавЛИіИљЮЊСэвЛИіИљЕФ2БЖЃЌдђГЦетбљЕФЗНГЬЮЊЁАБЖИљЗНГЬЁБЃЌвдЯТЙигкБЖИљЗНГЬЕФЫЕЗЈЃЌе§ШЗЕФЪЧ
________________ ЃЈаДГіЫљгае§ШЗЫЕЗЈЕФађКХЃЉ
ЂйЗНГЬx2-x-2=0ЪЧБЖИљЗНГЬЃЎ
ЂкШєЃЈx-2ЃЉЃЈmx+nЃЉ=0ЪЧБЖИљЗНГЬЃЌдђ4m2+5mn+n2=0ЃЛ
ЂлШєЕуЃЈpЃЌqЃЉдкЗДБШР§КЏЪ§y=![]() ЕФЭМЯѓЩЯЃЌдђЙигкxЕФЗНГЬpx2+3x+q=0ЪЧБЖИљЗНГЬЃЛ
ЕФЭМЯѓЩЯЃЌдђЙигкxЕФЗНГЬpx2+3x+q=0ЪЧБЖИљЗНГЬЃЛ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкбнГЊБШШќжаЃЌ5ЮЛЦРЮЏИјвЛЮЛИшЪжЕФДђЗжШчЯТЃК8.2ЗжЃЌ8.3ЗжЃЌ7.8ЗжЃЌ7.7ЗжЃЌ8.0ЗжЃЌдђетЮЛИшЪжЕФЦНОљЕУЗжЪЧЗжЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПИјГіЯТСаУќЬтЃК
(1)СНЬѕжБЯпБЛЕкШ§ЬѕжБЯпЫљНиЃЌЭЌЮЛНЧЯрЕШЃЛ
(2)ЯрЕШЕФНЧЪЧЖдЖЅНЧЃЛ
(3)ЭЌвЛЦНУцФкЃЌвЛЬѕжБЯпКЭСНЬѕЦНааЯпжаЕФвЛЬѕЯрНЛЃЌдђЫќгыСэвЛЬѕвВЯрНЛЃЛ
(4)ДгжБЯпЭтвЛЕуЕНетЬѕжБЯпЕФДЙЯпЖЮЃЌНазіИУЕуЕНжБЯпЕФОрРыЃЛ
(5)ВЛЯрНЛЕФСНЬѕжБЯпНазіЦНааЯп.
ЦфжаецУќЬтЕФИіЪ§ЪЧ( )
A. 0ИіB. 1ИіC. 2ИіD. 3Иі
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com