Question

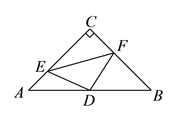
【题目】如图，在△ABC中，D为BC边的中点，过D点分别作DE∥AB交AC于点E，DF∥AC交AB于点F．

求证：BF=DE．

【答案】证明见解析

【解析】试题分析：根据两组对边分别平行的四边形为平行四边形可判定四边形AFDE是平行四边形，根据平行四边形的性质可得DE=AF，再由D为BC边的中点，DF∥AC，可得BF=AF，即可得BF=DE．

试题解析：

∵DE∥AB，DF∥AC，

∴DE∥AF，DF∥AE，

∴四边形AFDE是平行四边形，

∴DE=AF，

∵D为BC边的中点，

∴BD=DC，∵DF∥AC，

∴BF=AF，

∴BF=DE．

【题型】解答题
【结束】
26

【题目】如图，已知：∠C=∠D，OD=OC．求证：DE=CE．

Answer 1

【答案】证明见解析

【解析】试题分析：利用ASA证明△OBC≌△OAD，根据全等三角形的对应边相等可得OA=OB，再由OD=OC，即可得AC=BD，根据AAS证明△ACE≌△BDE，再由全等三角形的对应边相等即可得结论.

试题解析：

在△OBC和△OAD中，

，

∴△OBC≌△OAD（ASA），

∴OA=OB，

∵OD=OC，

∴OD﹣OB=OC﹣OA，即AC=BD，

在△ACE和△BDE中，

，

∴△ACE≌△BDE（AAS），

∴DE=CE．