
【题目】某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.若不够卡购物和使用优惠卡购物分别视为方式一购物和方式二购物,且设顾客购买商品的金额为![]() 元.
元.
(Ⅰ)根据题意,填写下表:
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … | |
方式二的总费用(元) | 540 | … |
(Ⅱ)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?
(Ⅲ)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(Ⅳ)小张按合算的方案,把这台冰箱买下,如果该商场还能盈利![]() ,那么这台冰箱的进价是多少元?
,那么这台冰箱的进价是多少元?
【答案】(Ⅰ)见解析;(Ⅱ)当顾客消费等于1500元时买卡与不买卡花钱相等;(Ⅲ)小张买卡(方式二购物)合算,能节省400元钱;(Ⅳ)这台冰箱的进价是2480元.
【解析】
(Ⅰ)根据花300元买这种卡后,凭卡可在这家商场按标价的8折购物,进行计算即可
(Ⅱ)根据花300元买这种卡后,凭卡可在这家商场按标价的8折购物,得出方程求出即可;
(Ⅲ)根据方案一:总费用=标价.方案二:费用=300 +标价![]() .据此可得出方案一和方案二总费用和购物金额之间的函数关系式,再得出当
.据此可得出方案一和方案二总费用和购物金额之间的函数关系式,再得出当![]() 时,y的值即可得出答案.
时,y的值即可得出答案.
(Ⅳ)首先假设进价为a元,则可得出(300+3500×0.8)-a=25%a进而求出即可.
解:(Ⅰ)
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … |
|
方式二的总费用(元) | 540 | 780 | 1100 | … |
|
(Ⅱ)顾客购买x元金额的商品时,买卡与不买卡花钱相等
根据题意,得![]() ,
,
解得:![]() ,
,
所以,当顾客消费等于1500元时买卡与不买卡花钱相等;
(Ⅲ)依题意可知:方式一购物的总费用为![]() ;
;
方式二购物的总费用为![]() ,
,
当![]() 时,
时,![]() (元);
(元);![]() (元);
(元);
∴![]() (元),
(元),
所以,小张买卡(方式二购物)合算,能节省400元钱;
(Ⅳ)设这台冰箱的进价为![]() 元,根据题意,(300+3500×0.8)-a=25%a
元,根据题意,(300+3500×0.8)-a=25%a
得:![]() .
.
答:这台冰箱的进价是2480元.


科目:初中数学 来源: 题型:
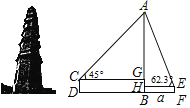
【题目】慈氏塔位于岳阳市城西洞庭湖边,是湖南省保存最好的古塔建筑之一.如图,小亮的目高CD为1.7米,他站在D处测得塔顶的仰角∠ACG为45°,小琴的目高EF为1.5米,她站在距离塔底中心B点a米远的F处,测得塔顶的仰角∠AEH为62.3°.(点D、B、F在同一水平线上,参考数据:sin62.3°≈0.89,cos62.3°≈0.46,tan62.3°≈1.9)
(1)求小亮与塔底中心的距离BD;(用含a的式子表示)
(2)若小亮与小琴相距52米,求慈氏塔的高度AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
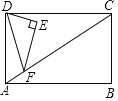
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本,每本价格为2元.在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为![]() 元,在乙文具店购买这种笔记本的付款金额为
元,在乙文具店购买这种笔记本的付款金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)当![]() 时,在哪家文具店购买这种笔记本的花费少?请说明理由.
时,在哪家文具店购买这种笔记本的花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 经过点A(-3,4).
经过点A(-3,4).
(1)求b的值;
(2)过点A作![]() 轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
轴的平行线交抛物线于另一点B,在直线AB上任取一点P,作点A关于直线OP的对称点C;
①当点C恰巧落在![]() 轴时,求直线OP的表达式;
轴时,求直线OP的表达式;
②连结BC,求BC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 是正方形,
是正方形,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
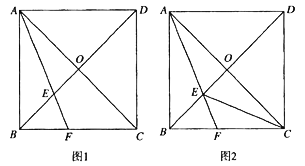
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3(a≠0),且a+b=3.
(1)若其图象经过点(﹣3,0),求此二次函数的表达式.
(2)若(m,n)为(1)中二次函数图象在第三象限内的点,请分别求m,n的取值范围.
(3)点P(x1,y1),Q(x2,y2)是函数图象上两个点,满足x1+x2=2且x1<x2,试比较y1和y2的大小关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点P在∠BCA平分线CD上,且PA=PB.
(1)用尺规作出符合要求的点P(保留作图痕迹,不需要写作法);
(2)判断△ABP的形状(不需要写证明过程)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将正面分别写着数字1,2,3的三张卡片(注:这三张卡片的形状、大小、质地、颜色等其它方面完全相同,若背面朝上放在桌面上,这三张卡片看上去无任何差别)洗匀后,背面朝上方在桌面上,甲从中随机抽取一张卡片,记该卡片上的数字为![]() ,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为
,然后放回洗匀,背面朝上方在桌面上,再由乙从中随机抽取一张卡片,记该卡片上的数字为![]() ,组成一数对
,组成一数对![]() .
.
(1)请写出![]() .所有可能出现的结果;
.所有可能出现的结果;
(2)甲、乙两人玩游戏,规则如下:按上述要求,两人各抽依次卡片,卡片上述资质和为奇数则甲赢,数字之和为偶数则乙赢,你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com