
【题目】已知四边形![]() 是正方形,
是正方形,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
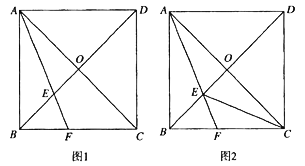
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
【答案】(1)见解析;(2)![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
【解析】
(1)取AF的中点G,连接OG,根据三角形的中位线得出OG=![]() FC,OG//FC,根据正方形的性质求出∠0AB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
FC,OG//FC,根据正方形的性质求出∠0AB、∠ABO、∠OCB的度数,求出∠OEA和∠OGF的度数,推出OG=OE即可;
(2)由已知条件和三角形内角和定理可得∠DAE=∠DEA,∠DEC=∠DCE,∠BEF=∠BFE,进而可得△DAE;△DCE;△BEF是等腰三角形,由垂直平分线的性质可得AE=CE进而可得△AEC是等腰三角形.
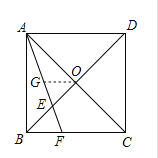
解:证明:(1)如图:取![]() 的中点G,连接OG.
的中点G,连接OG.
∵正方形![]() ,
,![]() 、
、![]() 交于点
交于点![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() 平分
平分![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
∴![]() .
.
(2)
∵四边形ABCD是正方形,
∴BD⊥AC,AO=CO,∠BAC=∠DAC=45°,
∴AE=CE,
∴△AEC是等腰三角形;
∵过点A作∠BAC的平分线分别交BD、BC于E、F,
∴∠BAF=∠CAF=22.5°,
∴∠DAE=67.5°,
∴∠AED=67.5°,
∴AD=ED,
∴△ADE是等腰三角形,AE=CE,
∵∠ECA=∠EAC=22.5°,
∴∠ECD=67.5°,
∴∠DEC=∠DCE=67.5°,
∴DE=CE,
∴△DEC是等腰三角形,
∵∠BEF=∠BFE=67.5°,
∴BE=BF,
∴△BEF是等腰三角形.
可直接写出图中所有的等腰三角形有:![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.
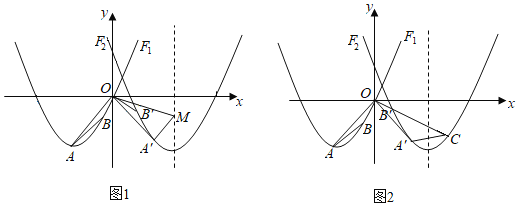
查看答案和解析>>
科目:初中数学 来源: 题型:
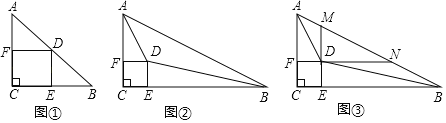
【题目】(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系;
(2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数;
(3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,BN的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
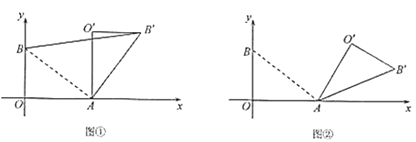
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(Ⅲ)记![]() 为
为![]() 的中点,S为
的中点,S为![]() 的面积,求S的取值范围(直接写出结果即可).
的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销活动,出售一种优惠购物卡(注:此卡只作为购物优惠凭证不能顶替货款),花300元买这种卡后,凭卡可在这家商场按标价的8折购物.若不够卡购物和使用优惠卡购物分别视为方式一购物和方式二购物,且设顾客购买商品的金额为![]() 元.
元.
(Ⅰ)根据题意,填写下表:
商品金额(元) | 300 | 600 | 1000 | … |
|
方式一的总费用(元) | 300 | 600 | 1000 | … | |
方式二的总费用(元) | 540 | … |
(Ⅱ)顾客购买多少元金额的商品时,买卡与不买卡花钱相等?
(Ⅲ)小张要买一台标价为3500元的冰箱,如何购买合算?小张能节省多少元钱?
(Ⅳ)小张按合算的方案,把这台冰箱买下,如果该商场还能盈利![]() ,那么这台冰箱的进价是多少元?
,那么这台冰箱的进价是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个斜抛物体的水平运动距离为x(m),对应的高度记为h(m),且满足h=ax2+bx﹣11a(其中a≠0).已知当x=0时,h=2;当x=10时,h=2.
(1)求h关于x的函数表达式.
(2)求斜抛物体的最大高度和达到最大高度时的水平距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
我们知道一次函数![]() (
(![]() ,
,![]() 是常数)的图象是一条直线,到高中学习时,直线通常写成
是常数)的图象是一条直线,到高中学习时,直线通常写成![]() (
(![]() ,
,![]() 是常数)的形式,点
是常数)的形式,点![]() 到直线
到直线![]() 的距离可用公式
的距离可用公式![]() 计算.
计算.
例如:求点![]() 到直线
到直线![]() 的距离.
的距离.
解:∵![]()
∴![]() 其中
其中![]()
∴点![]() 到直线
到直线![]() 的距离为:
的距离为:
![]()
根据以上材料解答下列问题:
(1)求点![]() 到直线
到直线![]() 的距离;
的距离;
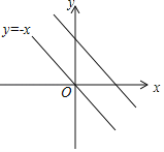
(2)如图,直线![]() 沿
沿![]() 轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
轴向上平移2个单位得到另一条直线,求这两条平行直线之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某出租公司有若干辆同一型号的货车对外出租,每辆货车的日租金实行淡季、旺季两种价格标准,旺季每辆货车的日租金比淡季上涨![]() .据统计,淡季该公司平均每天有
.据统计,淡季该公司平均每天有![]() 辆货车未出租,日租金总收入为
辆货车未出租,日租金总收入为![]() 元;旺季所有的货车每天能全部租出,日租金总收入为
元;旺季所有的货车每天能全部租出,日租金总收入为![]() 元.
元.
(1)该出租公司这批对外出租的货车共有多少辆?淡季每辆货车的日租金多少元?
(2)经市场调查发现,在旺季如果每辆货车的日租金每上涨![]() 元,每天租出去的货车就会减少
元,每天租出去的货车就会减少![]() 辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
辆,不考虑其它因素,每辆货车的日租金上涨多少元时,该出租公司的日租金总收入最高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】.已知:在矩形![]() 中,
中,![]() 是对角线,
是对角线,![]() 于点
于点![]() ,
,![]() 于点
于点![]() ;
;
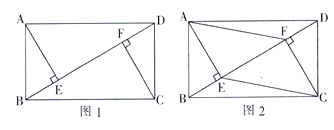
(1)如图1,求证:![]() ;
;
(2)如图2,当![]() 时,连接
时,连接![]() .
.![]() ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形
,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形![]() 面积的
面积的![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com