
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
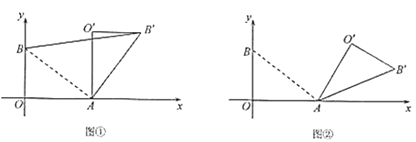
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(Ⅲ)记![]() 为
为![]() 的中点,S为
的中点,S为![]() 的面积,求S的取值范围(直接写出结果即可).
的面积,求S的取值范围(直接写出结果即可).
【答案】(Ⅰ)![]() ;(Ⅱ)点
;(Ⅱ)点![]() 的坐标为
的坐标为![]() ;(Ⅲ)
;(Ⅲ)![]() .
.
【解析】
(Ⅰ)利用勾股定理求出AB的长,根据旋转的性质可得∠BAB′=90°,AB=AB′,利用勾股定理求出BB′的长即可;(Ⅱ) 点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,由旋转的性质可得
,由旋转的性质可得![]() ,
,![]() .即可求出∠O′AC=60°,利用∠O′AC的三角函数可求出OC和AC的长,进而可得OC的长,即可得答案;(Ⅲ)由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,可得O′在AB上时S最小,O′在BA的延长线上时S最大,先求出KO′的长,进而求出S的值即可得答案.
.即可求出∠O′AC=60°,利用∠O′AC的三角函数可求出OC和AC的长,进而可得OC的长,即可得答案;(Ⅲ)由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,可得O′在AB上时S最小,O′在BA的延长线上时S最大,先求出KO′的长,进而求出S的值即可得答案.
(Ⅰ)∵点![]() ,点
,点![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,由勾股定理,得
中,由勾股定理,得![]() .
.
根据题意,![]() 是
是![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到的,
得到的,
由旋转的性质,可得![]() ,
,![]() .
.
∴在![]() 中,
中,![]() .
.
(Ⅱ)如图,根据题意,由旋转的性质,
可得![]() ,
,![]() .
.
过点![]() 作
作![]() 轴,垂足为
轴,垂足为![]() ,则
,则![]() .
.
在![]() 中,
中,
由![]() ,
,
得![]() ,
,
![]() .
.
有![]() .
.
∴点![]() 的坐标为
的坐标为![]() .
.
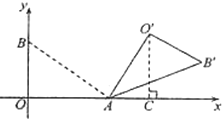
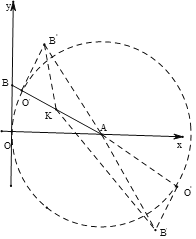
(Ⅲ)如图,由旋转的性质可得点O′在以A为圆心,AO为半径的圆上,且O′B′为圆的切线,
∴O′在AB上时S最小,O′在BA的延长线上时S最大,
当O′在AB上时,
∵K为AB中点,
∴AK=![]() ,
,
∴KO′=4-![]() =
=![]()
∴S=![]() ×
×![]() ×3=
×3=![]() ,
,
当O′在BA的延长线上时,KO′=AK+AO′=![]() +4=
+4=![]() ,
,
∴S=![]() ×
×![]() ×3=
×3=![]() ,
,
∴S的取值范围为:![]() ≤S≤
≤S≤![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
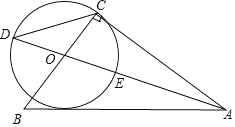
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AO交BC于点O,以O为圆心,OC长为半径作⊙O,⊙O交AO所在的直线于D、E两点(点D在BC左侧).
(1)求证:AB是⊙O的切线;
(2)连接CD,若AC=![]() AD,求tan∠D的值;
AD,求tan∠D的值;
(3)在(2)的条件下,若⊙O的半径为5,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数![]() 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)写出不等式kx+b>﹣![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本,每本价格为2元.在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为![]() 元,在乙文具店购买这种笔记本的付款金额为
元,在乙文具店购买这种笔记本的付款金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)当![]() 时,在哪家文具店购买这种笔记本的花费少?请说明理由.
时,在哪家文具店购买这种笔记本的花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级有900名学生,在体育考试前随机抽取部分学生进行跳绳测试,根据测试成绩制作了下面两个统计图.请根据相关信息,解答下列问题:
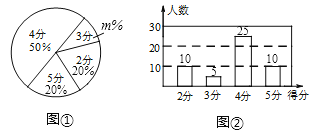
(Ⅰ)本次参加跳绳测试的学生人数为________,图①中![]() 的值为________;
的值为________;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数;
(Ⅲ)根据样本数据,估计该校九年级跳绳测试中,成绩超过3分的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 是正方形,
是正方形,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
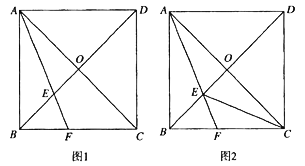
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“书香八桂,阅读圆梦”读书活动中,某中学设置了书法、国学诵读、演讲、征文四个比赛项目(每人只参加一个项目),九(2)班全班同学都参加了比赛,该班班长为了了解本班同学参加各项比赛的情况,收集整理数据后,绘制以下不完整的折线统计图(图1)和扇形统计图(图2),根据图表中的信息解答下列各题:
(1)请求出九(2)全班人数;
(2)请把折线统计图补充完整;
(3)南南和宁宁参加了比赛,请用“列表法”或“画树状图法”求出他们参加的比赛项目相同的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某射箭队准备从王方、李明二人中选拔1人参加射箭比赛,在选拔赛中,两人各射箭10次的成绩(单位:环数)如下:
次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
王方 | 7 | 10 | 9 | 8 | 6 | 9 | 9 | 7 | 10 | 10 |
李明 | 8 | 9 | 8 | 9 | 8 | 8 | 9 | 8 | 10 | 8 |
(1)根据以上数据,将下面两个表格补充完整:
王方10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 | |
频数 | ______ | ______ | ______ | ______ | ______ | |
频率 | ______ | ______ | ______ | ______ | ______ |
李明10次射箭得分情况
环数 | 6 | 7 | 8 | 9 | 10 |
频数 | ______ | ______ | ______ | ______ | ______ |
频率 | ______ | ______ | ______ | ______ | ______ |
(2)分别求出两人10次射箭得分的平均数;
(3)从两人成绩的稳定性角度分析,应选派谁参加比赛合适.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com