
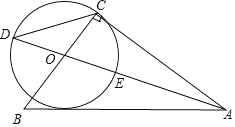
【题目】如图,在Rt△ABC中,∠ACB=90°,∠BAC的平分线AO交BC于点O,以O为圆心,OC长为半径作⊙O,⊙O交AO所在的直线于D、E两点(点D在BC左侧).
(1)求证:AB是⊙O的切线;
(2)连接CD,若AC=![]() AD,求tan∠D的值;
AD,求tan∠D的值;
(3)在(2)的条件下,若⊙O的半径为5,求AB的长.
【答案】(1)证明见解析;(2)tan∠D=![]() ;(3)AB=
;(3)AB=![]() .
.
【解析】
(1)如图,过点O作OF⊥AB,,求出OC=OF,证明OF为⊙O半径,且OF⊥AB,即可求解;
(2)连接CE,根据∠ACE=∠D,且∠A=∠A,求出△ACE∽△ADC,可得![]() ,即可求解;
,即可求解;
(3)根据△ACE∽△ADC,得![]() ,根据AO=AO,OC=OF,证明Rt△AOF≌Rt△AOC,求出AF=AC=12,根据∠B=∠B,∠OFB=∠ACB=90°,证明△OBF∽△ABC,可得
,根据AO=AO,OC=OF,证明Rt△AOF≌Rt△AOC,求出AF=AC=12,根据∠B=∠B,∠OFB=∠ACB=90°,证明△OBF∽△ABC,可得
![]() ,求出BF,即可求解.
,求出BF,即可求解.
证明:(1)如图,过点O作OF⊥AB,

∵AO平分∠BAC,OF⊥AB,∠ACB=90°
∴OC=OF,
∴OF为⊙O半径,且OF⊥AB
∴AB是⊙O切线.
(2)连接CE

∵DE是直径
∴∠DCE=90°
∵∠ACB=90°
∴∠DCE=∠ACB
∴∠DCO=∠ACE
∵OC=OD
∴∠D=∠DCO
∴∠ACE=∠D,且∠A=∠A
∴△ACE∽△ADC
∴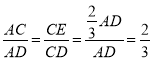
∴tan∠D=![]() =
=![]()
(3)∵△ACE∽△ADC
∴![]()
∴AC2=AD(AD﹣10),且AC=![]() AD
AD
∴AD=18
∴AC=12
∵AO=AO,OC=OF
∴Rt△AOF≌Rt△AOC(HL)
∴AF=AC=12
∵∠B=∠B,∠OFB=∠ACB=90°
∴△OBF∽△ABC
∴![]()
即![]()
∴![]()
∴BF=![]()
∴AB=FA+BF=12+![]() =
=![]()


科目:初中数学 来源: 题型:
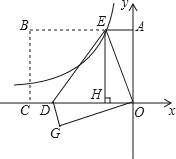
【题目】如图,在直角坐标系中,矩形OABC的顶点C在x轴的负半轴上,点A在y轴正半轴上,矩形OABC的面积为8![]() .把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=
.把矩形OABC沿DE翻折,使点B与点O重合,点C落在第三象限的G点处,作EH⊥x轴于H,过E点的反比例函数y=![]() 图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
图象恰好过DE的中点F.则k=_____,线段EH的长为:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
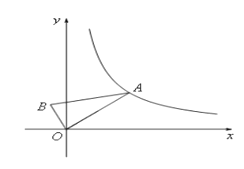
【题目】如图,Rt△OAB的顶点O与坐标原点重合,∠AOB=90°,AO=2BO,当A点在反比例函数![]() (x>0)的图象上移动时,B点坐标满足的函数解析式为( )
(x>0)的图象上移动时,B点坐标满足的函数解析式为( )
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
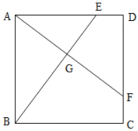
【题目】如图,正方形ABCD,点E,F分别在AD,CD上,且DE=CF,AF与BE相交于点G.
(1)求证:BE=AF;
(2)若AB=4,DE=1,求AG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:a*b=![]() ,则下列等式中对于任意实数 a、b、c 都成立的是( )
,则下列等式中对于任意实数 a、b、c 都成立的是( )
①a+(b*c)=(a+b)*(a+c) ②a*(b+c)=(a+b)*c
③a*(b+c)=(a*b)+(a*c) ④(a*b)+c= ![]() +(b*2c)
+(b*2c)
A. ①②③ B. ①②④ C. ①③④ D. ②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为拓展学生视野,促进书本知识与生活实践的深度融合,荆州市某中学组织八年级全体学生前往松滋洈水研学基地开展研学活动.在此次活动中,若每位老师带队14名学生,则还剩10名学生没老师带;若每位老师带队15名学生,就有一位老师少带6名学生,现有甲、乙两种大型客车,它们的载客量和租金如表所示:
甲型客车 | 乙型客车 | |
载客量(人/辆) | 35 | 30 |
租金(元/辆) | 400 | 320 |
学校计划此次研学活动的租金总费用不超过3000元,为安全起见,每辆客车上至少要有2名老师.
(1)参加此次研学活动的老师和学生各有多少人?
(2)既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,可知租车总辆数为 辆;
(3)学校共有几种租车方案?最少租车费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,△AOB的三个顶点A、O、B分别落在抛物线F1:![]() 的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
的图象上,点A的横坐标为﹣4,点B的纵坐标为﹣2.(点A在点B的左侧)
(1)求点A、B的坐标;
(2)将△AOB绕点O逆时针旋转90°得到△A'OB',抛物线F2:![]() 经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
经过A'、B'两点,已知点M为抛物线F2的对称轴上一定点,且点A'恰好在以OM为直径的圆上,连接OM、A'M,求△OA'M的面积;
(3)如图2,延长OB'交抛物线F2于点C,连接A'C,在坐标轴上是否存在点D,使得以A、O、D为顶点的三角形与△OA'C相似.若存在,请求出点D的坐标;若不存在,请说明理由.
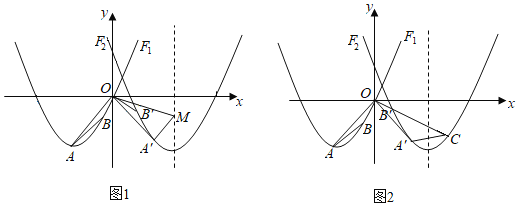
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知⊙O外一点P向⊙O作切线PA,点A为切点,连接PO并延长交⊙O于点B,连接AO并延长交⊙O于点C,过点C作![]() ,分别交PB于点E,交⊙O于点D,连接AD.
,分别交PB于点E,交⊙O于点D,连接AD.

(1)求证:△APO~△DCA;
(2)如图2,当![]() 时
时
①求![]() 的度数;
的度数;
②连接AB,在⊙O上是否存在点Q使得四边形APQB是菱形.若存在,请直接写出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,点
为原点,点![]() ,点
,点![]() ,把
,把![]() 绕点
绕点![]() 顺时针旋转,得
顺时针旋转,得![]() ,点
,点![]() ,
,![]() 旋转后的对应点为
旋转后的对应点为![]() ,
,![]() .记旋转角为
.记旋转角为![]() .
.
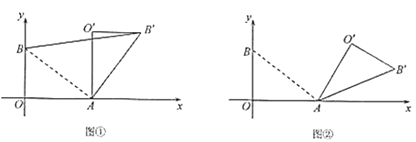
(Ⅰ)如图①,若![]() ,求
,求![]() 的长;
的长;
(Ⅱ)如图②,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(Ⅲ)记![]() 为
为![]() 的中点,S为
的中点,S为![]() 的面积,求S的取值范围(直接写出结果即可).
的面积,求S的取值范围(直接写出结果即可).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com