
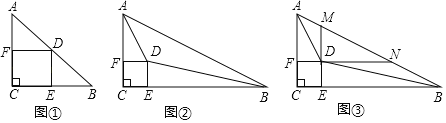
【题目】(1)数学理解:如图①,△ABC是等腰直角三角形,过斜边AB的中点D作正方形DECF,分别交BC,AC于点E,F,求AB,BE,AF之间的数量关系;
(2)问题解决:如图②,在任意直角△ABC内,找一点D,过点D作正方形DECF,分别交BC,AC于点E,F,若AB=BE+AF,求∠ADB的度数;
(3)联系拓广:如图③,在(2)的条件下,分别延长ED,FD,交AB于点M,N,求MN,AM,BN的数量关系.
【答案】数学理解:(1)AB=![]() (AF+BE),理由见解析;问题解决:(2)∠ADB=135°;联系拓广:(3)MN2=AM2+NB2,
(AF+BE),理由见解析;问题解决:(2)∠ADB=135°;联系拓广:(3)MN2=AM2+NB2,
【解析】
数学理解:
(1)由等腰直角三角形的性质可得AC=BC,∠A=∠B=45°,AB=![]() AC,由正方形的性质可得DE=DF=CE,∠DFC=∠DEC=90°,可求AF=DF=CE,即可得AB=
AC,由正方形的性质可得DE=DF=CE,∠DFC=∠DEC=90°,可求AF=DF=CE,即可得AB=![]() (AF+BE);
(AF+BE);
问题解决:
(2)延长AC,使FM=BE,通过证明△DFM≌△DEB,可得DM=DB,通过△ADM≌△ADB,可得∠DAC=∠DAB=![]() ∠CAB,∠ABD=∠CBD=
∠CAB,∠ABD=∠CBD=![]() ∠ABC,由三角形内角和定理可求∠ADB的度数;
∠ABC,由三角形内角和定理可求∠ADB的度数;
联系拓广:
(3)由正方形的性质可得DE∥AC,DF∥BC,由平行线的性质可得∠DAB=∠ADM,∠NDB=∠ABD,可得AM=MD,DN=NB,即可求MN,AM,BN的数量关系.
数学理解:
(1)AB=![]() (AF+BE)
(AF+BE)
理由如下:∵△ABC是等腰直角三角形
∴AC=BC,∠A=∠B=45°,AB=![]() AC
AC
∵四边形DECF是正方形
∴DE=DF=CE=CF,∠DFC=∠DEC=90°
∴∠A=∠ADF=45°
∴AF=DF=CE
∴AF+BE=BC=AC
∴AB=![]() (AF+BE)
(AF+BE)
问题解决:
(2)如图②,延长AC,使FM=BE,连接DM,
∵四边形DECF是正方形
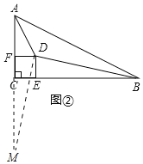
∴DF=DE,∠DFC=∠DEC=90°
∵BE=FM,∠DFC=∠DEB=90°,DF=ED
∴△DFM≌△DEB(SAS)
∴DM=DB
∵AB=AF+BE,AM=AF+FM,FM=BE,
∴AM=AB,且DM=DB,AD=AD
∴△ADM≌△ADB(SSS)
∴∠DAC=∠DAB=![]() ∠CAB
∠CAB
同理可得:∠ABD=∠CBD=![]() ∠ABC
∠ABC
∵∠ACB=90°,
∴∠CAB+∠CBA=90°
∴∠DAB+∠ABD=![]() (∠CAB+∠CBA)=45°
(∠CAB+∠CBA)=45°
∴∠ADB=180°﹣(∠DAB+∠ABD)=135°
联系拓广:
(3)∵四边形DECF是正方形
∴DE∥AC,DF∥BC
∴∠CAD=∠ADM,∠CBD=∠NDB,∠MDN=∠AFD=90°
∵∠DAC=∠DAB,∠ABD=∠CBD
∴∠DAB=∠ADM,∠NDB=∠ABD
∴AM=MD,DN=NB
在Rt∠DMN中,MN2=MD2+DN2,
∴MN2=AM2+NB2.


科目:初中数学 来源: 题型:
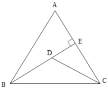
【题目】如图,△ABC中,AB=AC=10,tanA=2,BE⊥AC于点E,D是线段BE上的一个动点,则![]() 的最小值是( )
的最小值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 10
D. 10
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按要求解答下列各题:
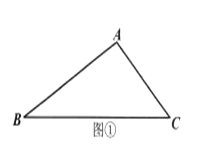
(1)如图①,求作一点![]() ,使点
,使点![]() 到
到![]() 的两边的距离相等,且在
的两边的距离相等,且在![]() 的边
的边![]() 上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
上.(用直尺和圆规作图,保留作图痕迹,不写作法和证明);
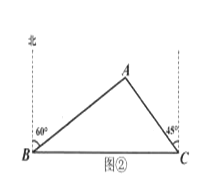
(2)如图②,![]() 表示两个港口,港口
表示两个港口,港口![]() 在港口
在港口![]() 的正东方向上.海上有一小岛
的正东方向上.海上有一小岛![]() 在港口
在港口![]() 的北偏东
的北偏东![]() 方向上,且在港口
方向上,且在港口![]() 的北偏西
的北偏西![]() 方向上.测得
方向上.测得![]() 海里,求小岛
海里,求小岛![]() 与港口
与港口![]() 之间的距离.(结果可保留根号)
之间的距离.(结果可保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k,b为常数,k≠0)的图象与反比例函数![]() 的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
的图象交于A、B两点,且与x轴交于点C,与y轴交于点D,A点的横坐标与B点的纵坐标都是3.
(1)求一次函数的表达式;
(2)求△AOB的面积;
(3)写出不等式kx+b>﹣![]() 的解集.
的解集.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,∠DCA=30°,点F是对角线AC上的一个动点,连接DF,以DF为斜边作∠DFE=30°的直角三角形DEF,使点E和点A位于DF两侧,点F从点A到点C的运动过程中,点E的运动路径长是________.
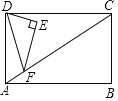
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实数a,b,c,用M{a,b,c}表示这三个数的平均数,用min{a,b,c}表示这三个数中最小的数.例如:M{1,2,9}=![]() =4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
=4,min{1,2,﹣3}=﹣3,min{3,1,1}=1.请结合上述材料,解决下列问题:
(1)①M{(﹣2)2,22,﹣22}= ; ②min{sin30°,cos60°,tan45°}= ;
(2)若M{﹣2x,x2,3}=2,求x的值;
(3)若min{3﹣2x,1+3x,﹣5}=﹣5,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司要购买一种笔记本供员工学习时使用.在甲文具店不管一次购买多少本,每本价格为2元.在乙文具店购买同样的笔记本,一次购买数量不超过20时,每本价格为2.4元;一次购买数量超过20时,超过部分每本价格为1.8元.
设在同一家文具店一次购买这种笔记本的数量为x(x为非负整数).
(Ⅰ)根据题意,填写下表:
一次购买数量(本) | 10 | 20 | 30 | 40 | … |
甲文具店付款金额(元) | 20 | 60 | … | ||
乙文具店付款金额(元) | 24 | 66 | … |
(Ⅱ)设在甲文具店购买这种笔记本的付款金额为![]() 元,在乙文具店购买这种笔记本的付款金额为
元,在乙文具店购买这种笔记本的付款金额为![]() 元,分别写出
元,分别写出![]() ,
,![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(Ⅲ)当![]() 时,在哪家文具店购买这种笔记本的花费少?请说明理由.
时,在哪家文具店购买这种笔记本的花费少?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 是正方形,
是正方形,![]() 、
、![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 的平分线分别交
的平分线分别交![]() 、
、![]() 于点
于点![]() 、
、![]() .
.
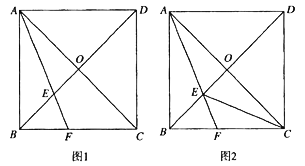
(1)如图![]() ,求证:
,求证:![]() ;
;
(2)如图![]() ,连接
,连接![]() ,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
,在不添加其他字母和辅助线的条件下,直接写出图中所有的等腰三角形(等腰直角三角形除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() +b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
+b(a、b为常数且a≠0)中,当x=2时,y=4;当x=﹣1时,y=1.请对该函数及其图象进行如下探究:
(1)求该函数的解析式,并直接写出该函数自变量x的取值范围;
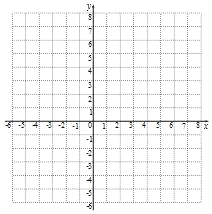
(2)请在下列直角坐标系中画出该函数的图象;
(3)请你在上方直角坐标系中画出函数y=2x的图象,结合上述函数的图象,写出不等式![]() +b≤2x的解集.
+b≤2x的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com